kuniga.me > NP-Incompleteness > The Open Mapping Theorem

The Open Mapping Theorem

24 Dec 2024

Abstract representation of a map from an open disk to another.

This is the 9th post in the series with my notes on complex integration, corresponding to Chapter 4 in Ahlfors’ Complex Analysis.

In today’s post we’ll go over the Open mapping theorem, which states that if the domain of a non-constant holomorphic functions is open, then its image is open too.

The previous posts from the series:

Formal Statement

The open mapping theorem states that if $f : \Omega \rightarrow \mathbb{C}$ is a non-constant holomorphic function, then for any open subset $Z$ of $\Omega$, the image $f(Z)$ is open.

We note that this property doesn’t hold for the real case. For example, if we have $f(x) = x^2$, $x \in \mathbb{R}$, for the open interval $(-1, 1)$ we obtain the non-open interval $[0, 1)$.

An interesting thing about this theorem is that its proof relies on results that don’t seem, at a first glance, related to open sets: the zeros of a function.

We’ll now go over a few smaller lemmas that will lead to the open mapping theorem. Their proofs are hidden by default, but hopefully the lemmas statements give a good sense on the overall structure of the proof.

Zeros

In the last post, we learned about zeros and poles. Turns out they play a key role in the open mapping theorem.

Recall that a zero of a function $f(z)$ is a value $z_0$ for which $f(z_0) = 0$. It has order $m$ if all the derivatives up to $m-1$ are also zero, i.e. $f^{(k)}(z_0) = 0$, but the $m$-th derivative is not, i.e. $f^{(m)}(z_0) \ne 0$.

We start with a Lemma that lets us factorize our function $f(z)$ in order to obtain another that is “zero-free”.

Lemma 1. Let $f(z)$ be a holomorphic function in $\Omega$ and $z_1, z_2, \cdots, z_n$ be its zeros, and $m_1, m_2, \cdots, m_n$ their order.

Then $f(z)$ can be written as:

\[(1) \quad f(z) = (z - z_1)^{m_1}(z - z_2)^{m_2} \cdots (z - z_n)^{m_n} g(z)\]

Where $g(z)$ is a holomorphic function that is never 0.

We use the result that holomorphic functions are analytic [2], and can thus be written as a Taylor series: $$f(z) = c_0 + c_1 (z - a) + c_2 (z - a)^2 \cdots$$ for some disk centered in $a$. If we choose $a = z_1$, since $z_1$ is a zero of $f$, we have $f(z_1) = 0$ and thus $c_0 = 0$.

If $z_1$ has order greater than one, then $f'(z_1) = 0$. Differentiating the Taylor series: $$f'(z) = c_1 + 2 c_2 (z - z_1) + 3 c_3 (z - z_1)^2 + \cdots$$ From $f'(z_1) = 0$ we conclude that $c_1 = 0$. We can repeat this process $m_1$ times to conclude that the first $m_1 - 1$ coefficients are 0: $$f(z) = c_{m_1} (z - z_1)^{m_1} + c_{m_1 + 1} (z - z_1)^{m_1 + 1} + \cdots$$ So we can write $$(1.1) \quad f(z) = (z - z_1)^{m_1} f_1(z)$$ for some holomorphic function $f_1(z)$. We claim that $f_1(z_1) \ne 0$. This is so because: $$f^{(m_1)}(z) = m_1! f_1(z)$$ So if $f_1(z_1) = 0$, then $f^{(m_1)}(z_1) = 0$, implying that $z_1$ has order $m_1 + 1$, a contradiction.

Now, given that $z_2 \ne z_1$, having $f(z_2) = 0$ implies that $f_1(z_2) = 0$ by $(1.1)$. Thus we use the same argument to conclude that: $$f_1(z) = (z - z_2)^{m_2} f_2(z)$$ We can also see that neither $z_1$ nor $z_2$ are zeros of $f_2(z)$. Repeating up until $n$, should give us the desired result, where $g(z)$ has none of the zeros $z_1, z_2, \cdots, z_n$. It also should not contain any other zero $z'$, because it would imply that $f(z') = 0$. QED

This result reminds me of the Fundamental theorem of algebra in which a polynomial can be expressed as a product of its zeros.

Winding Number

Recall that given a closed curve $\gamma$, the function $n(\gamma, a)$, the winding number of $a$ with respect to $\gamma$, corresponds to how many times the curve $\gamma$ winds around the point $a \not \in \gamma$. If $\gamma$ is a simple closed curve (aka Jordan curve), then $\gamma$ can wind around $a$ at most once, so $n(\gamma, a)$ can tell whether $a$ is inside ($n(\gamma, a) = 1$) or outside of $\gamma$ ($n(\gamma, a) = 0$).

We now make a connection between zeros and winding numbers:

Lemma 2. Let $f(z)$ be a non-constant holomorphic function in $\Omega$ and $z_1, z_2, \cdots, z_n$ be its zeros, and $m_1, m_2, \cdots, m_n$ their order. Let $\gamma$ be a closed curve in $\Omega$ and $n(\gamma, a)$ the winding number of a point $a$ with respect to $\gamma$. Let $\Gamma$ be the image of $f(\gamma)$. Then:

\[(2) \quad n(\Gamma, 0) = \sum_{i = 1}^{n} n(\gamma, z_i) m_i\] Let $w = f(z)$, so that $\frac{dw}{dz} = f'(z)$ or $f'(z)dz = dw$. Using change of variables we can write: $$\int_\gamma \frac{f'(z)}{f(z)}dz = \int_\Gamma \frac{1}{w}dw$$ The definition of the winding number $n(\Gamma, 0)$ is [5]: $$ n(\Gamma, 0) = \frac{1}{2\pi i} \int_{\Gamma} \frac{1}{z - 0} dw $$ Thus: $$ n(\Gamma, 0) = \frac{1}{2\pi i} \int_\gamma \frac{f'(z)}{f(z)}dz = \sum_{i = 1}^n n(\gamma, z_i) m_i $$

Some comments about this result:

The requirement that $f(z)$ is non-constant is so that $\Gamma$ is a closed curve. Otherwise it would degenerate into an isolated point.
Recall that the winding number function returns integers, so all terms in equation $(2)$ involve integers.
If we count a zero $z(a)_i$ inside $\gamma$, we account for all its orders (we can’t have partial counts).

If $\gamma$ is a Jordan curve, we can interpret the equation as saying: the number of times $\Gamma$ winds around $0$ in the “$w$-plane” tells us how many of the zeros of $f(z)$ are contained inside $\gamma$ in the “$z$-plane”.

Now, what if we replace $0$ by $a$ in $n(\Gamma, 0)$? What does $n(\Gamma, a)$ represent? It turns out it tells us how many values that make $f(z) = a$ are inside $\gamma$. So the result we obtained is just a special case for $a = 0$!

A more formal way to state this result is that $n(\Gamma, a)$ tells us how many of the zeros of $g(z) = f(z) - a$ are inside $\gamma$. So in a sense Lemma 2 is invariant with translation:

Lemma 3. Let $f(z)$ be a non-constant holomorphic function in $\Omega$ and $z(a)_1, z(a)_2, \cdots, z(a)_n$ be the zeros of $f(z) - a$, and $m(a)_1, m(a)_2, \cdots, m(a)_n$ their order. Let $\gamma$ be a closed curve in $\Omega$ and $n(\gamma, a)$ the winding number of a point $a$ with respect to $\gamma$. Let $\Gamma$ be the image of $f(\gamma)$. Then:

\[(3) \quad \sum_{i = 1}^n n(\gamma, z(a)_i) m(a)_i = n(\Gamma, a)\] Let $g(z) = f(z) - a$. We can apply Lemma 2 for $g(z)$ to conclude: $$ \sum_{i = 1}^n n(\gamma, z(a)_i) m(a)_i = \int_\gamma \frac{f'(z)}{f(z) - a} dz $$ We have $g'(z) = f'(z) = dw/dz$, so doing a change of variables gives us: $$ \int_\gamma \frac{f'(z)}{f(z) - a} dz = \int_\Gamma \frac{1}{w - a}dw = n(\Gamma, a) 2 \pi i $$ Which shows that: $$ n(\Gamma, a) = \sum_{i = 1}^n n(\gamma, z(a)_i) m(a)_i $$

Recall Lemma 4 in The Winding Number [5], which claims that points in the same region (defined by $\Gamma$) share the same winding number. This means that if points $a$ and $b$ are in the same region with respect to $\Gamma$, then $\gamma$ contains the same number of zeros of $f(z) - a$ and $f(z) - b$, per Lemma 3 above. More formally:

Lemma 4. Let $f(z)$ be a non-constant holomorphic function in $\Omega$, a Jordan curve $\gamma$ inside $\Omega$, and $z_0$ a point not in $\gamma$. Define $w_0 = f(z_0)$ so that $z_0$ is a zero of $f(z_0) - w_0$. Let $\Gamma$ be image of $f(\gamma)$.

Then there exists a disk $B = \curly{\abs{w - w_0} \lt \delta}$, $\delta \gt 0$ such that for any $a \in B$, $\gamma$ contains the same of number zeros of $f(z) - a$ as it does of $f(z_0) - w_0$.

Because $z_0$ is not in $\gamma$, then $w_0$ is not in $\Gamma$, and since $\Gamma$ is a closed set, its complement is open and thus there exists a disk centered in $w_0$, $\abs{w - w_0} \le \delta$ that does not intersect $\Gamma$, which means all points in $B$ are within the same region defined by $\Gamma$.

From Lemma 4 in [5], we have that points in the same region (defined by $\Gamma$) share the same winding number. Thus we can conclude for any $a \in B$ the function $f(z) - a$ has the same number of zeros inside $\gamma$ as $f(z) - w_0$.

Note that it doesn’t mean that $f(z) - a$ and $f(z) - w_0$ have the same number of zeros, only that those inside $\gamma$ are the same.

Before we proceed to the open mapping theorem, let’s take a quick detour and mention Rouché’s theorem.

Rouché’s theorem

In the preceding section, we connected the number of zeros of two functions $f(z) - a$ and $f(z) - w_0$, as long as $a$ is sufficiently close to $w_0$. An alternative way to connect the number of zeros of two functions is by Rouché’s theorem (which we won’t prove here).

Theorem 5. (Rouché’s theorem) Let $f(z)$ and $g(z)$ be holomorphic functions in a region $K$ and let $\delta K$ be its closed countour. If $\abs{g(z)} \lt \abs{f(z)}$ for $z \in \delta K$, then $f$ and $f + g$ have the same number of zeros inside $\delta K$.

Another way to state Theorem 5 is that if we have $\abs{f(z) - g(z)} \lt \abs{f(z)}$ for $z \in \delta K$, then $f$ and $g$ have the same number of zeros inside $\delta K$.

We can use this theorem to obtain Lemma 4. Let $K$ be the region defined by $\gamma$ and its interior, so that $\delta K = \gamma$. Leg $g(z)$ in the theorem be our $f(z) - a$ and $f(z)$ in the theorem be our $f(z) - w_0$, so that $g(z) - f(z) = a - w_0$.

Like in Lemma 4, we assume that circle $B = \curly{\abs{w - w_0} \lt \epsilon}$ is contained in $\Gamma = f(\gamma)$. This means that for $z \in \gamma$, we have that $\abs{f(z) - w_0} \gt \delta$ because $f(z)$ lies outside $B$. We choose $a$ from inside $B$, which implies $\abs{a - w_0} \lt \delta$, so $\abs{f(z) - g(z)} \lt \abs{f(z)}$ and we can apply Rouché’s theorem and we arrive at the same conclusion as Lemma 4.

End of the detour. Let’s go back to proving the open mapping theorem.

Open Mapping

Another way of saying “$\gamma$ contains a zero of the function $f(z) - a$” is to say $\gamma$ contains a value $z_a$ such that $f(z_a) = a$. What Lemma 4 tells us is that if there some $b$ close enough to $a$, it’s guaranteed that $\gamma$ also contains a $z_b$ such that $f(z_b) = b$! Lemma 6 expands and formalizes this idea:

Lemma 6. Let $f: \Omega \rightarrow \mathbb{C}$ a non-constant holomorphic function in $\Omega$. Then for each $z_0 \in \Omega$, there exists an open disk $D = \curly{\abs{z - z_0} \lt \epsilon}$ (contained in $\Omega$) and an open disk $B = \curly{\abs{w - f(z_0)} \lt \delta}$ such that for every $a \in B$, there’s a corresponding $z_a \in D$ for which $f(z_a) = a$.

In Lemma 4, we assume $\gamma = D$, so it says there exists a open disk $B = \curly{\abs{w - w_0} \lt \delta}$ such that for all $a \in B$, $f(z) - a$ has the same number of zeros in $D$ as does $f(z) - w_0$. Since $z_0$ is a zero of $f(z) - w_0$, there's at least one zero of $f(z) - w_0$ in $D$ and thus of $f(z) - a$ in $D$. Let $z_a \in D$ be such that $f(z_a) = a$.

In other words, the inverse image of $B$, $f^{-1}(B)$, is contained in $D$, which in turn implies that $B$ is contained in $f(D)$. Since $D \subseteq \Omega$, then $f(D) \subseteq f(\Omega)$, thus $B \subseteq f(\Omega)$. So for every $w_0 \in f(\Omega)$, there is $z_0$ such that $f(z_0) = w_0$, which implies that there exists an open disk around $w_0$ contained in $f(\Omega)$ which implies $f(\Omega)$ is open.

This proves the open mapping theorem:

Theorem 7. (Open Mapping Theorem) A non-constant holomorphic function maps open sets to open sets.

Refined Analysis

Now let’s take a closer look at the nature of $f(z)$, in particular in the case where its image is a disk, as we have considered in Lemma 6.

In Lemma 6, we chose an open disk $D = \curly{\abs{z - z_0} \lt \epsilon}$ such that it contains at least one zero of $f(z) - w_0$, in that case $z_0$. It’s possible there are other values for which $f(z) = w_0$, but we can shrink $D$ enough to make sure $z_0$ is the only zero. Let $m$ be the order of $z_0$.

If $m = 1$, Lemma 8 shows that locally, $f(z)$ is a bijective and conformal function:

Lemma 8. Let $f(z)$ be a non-constant holomorphic function in an open disk $D$ centered at $z_0$, with $z_0$ being the only zero of $f(z) - w_0$, and of order 1.

Then there exists an open disk $B$ centered in $w_0$ such that $f$ is a bijection between $f^{-1}(B)$ and $B$. For this domain, $f$ is also conformal, and $f^{-1}$ is holomorphic.

Let $g(z) = f(z) - w_0$. Since $m = 1$, by definition $g'(z_0) \ne 0$ and we have that $g'(z_0) = f'(z_0)$. This also means that $n(\Gamma, 0) = 1$ and so is $n(\Gamma, a)$ for $a \in B$, which means only one $z_a$ exists in $D$ such that $f(z_a) = a$. Since we count the order of zeros in $n(\Gamma, a)$, it implies that $z_a$ has order 1, and thus that $f'(z_a) \ne 0$. We conclude that $f(z)$ is a bijection because for every $a$ in $B$ there's exactly one $z_a$ in $f^{-1}(B)$. Since $f'(z) \ne 0$ for all $z \in f^{-1}(B)$, by *Theorem 3* in [7] that $f$ is conformal map in $f^{-1}(B)$. It can also be shown, via the Holomorphic inverse function theorem that $f^{-1}$ is holomorphic at $f^{-1}(B)$. Summarizing as a corollary:

For the case where $m > 1$ the function is not as simple, but we can decompose it into two: a bijective function and a simple power function:

Lemma 9. Let $f(z)$ be a non-constant holomorphic function in an open disk $D$ centered at $z_0$, with $z_0$ being the only zero of $f(z) - w_0$, and of order greater than 1.

Then there exists a bijective and conformal function $\xi(z)$ such that

\[(4) \quad f(z) - w_0 = \xi(z)^m\] We have that $z_0$ is the only zero of $f(z) - w_0$ and has order $m$, so we can use Lemma 1 to obtain: $$ (9.1) f(z) - w_0 = (z - z_0)^m g(z) $$ Where $g(z)$ is a holomorphic function that has no zeros in the open disk $D$. Now consider $g(z)^{1/m}$. This is a multi-valued function, but we can obtain a single valued one via branch cutting [8]. The branch cut we use is the usual negative real axis. So as long as the $g(z)$ doesn't intersect the branch cut, we can pick an arbitrary branch of $g(z)^{1/m}$.

Since $g(z)$ is holomorphic, it's also continuous. To recap, that means that for any $\epsilon \gt 0$, there exists $\delta \gt 0$ such that $\abs{g(z) - g(z_0)} \lt \epsilon$ for all $\abs{z - z_0} \lt \delta$. In other words, we can make the difference $\abs{g(z) - g(z_0)}$ arbitrarily small by shrinking $\delta$. In particular, if we set $\epsilon = \abs{g(z_0)}$, we can guarantee that: $$\abs{g(z) - g(z_0)} \lt g(z_0)$$ This effectively indicates that $g(z)$ doesn't cross the real-axis and thus avoids the branch cut. We can thus pick an arbitrary branch $h(z) = g(z)^{1/m}$ which is single valued and holomorphic.

Now we define $\xi(z) = (z - z_0)h(z)$, which is holomorphic. We have that $\xi(z)$ is not constant because $\xi'(z) = h(z)$ and since $g(z) \ne 0$, $h(z) \ne 0$. Finally we have that $\xi(z_0) = 0$. So we can apply Lemma 8 for $f(z) = \xi(z)$ and $w_0 = 0$, to conclude that there's an open disk $B'$ centered at the origin such that $\xi(z)$ is a bijection between $\xi^{-1}(B')$ and $B$.

By replacing the definition of $\xi$ in $(9.1)$ we obtain $(4)$.

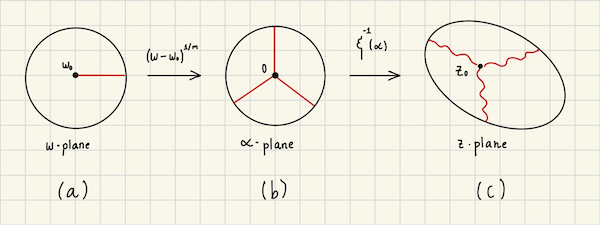
We can visualize what $w = f(z)$ does in the case $m \gt 1$. We’ll actually consider the inverse function, so we express $z$ as function of $w$ via:

\[z = \xi^{-1}((w - w_0)^{1/m})\]

We know that $\xi^{-1}$ is holomorphic and conformal from Lemma 9. Consider a disk centered in $w_0$ of radius $\delta$ in the $w$-space. Let’s observe what happens to a set of points along a ray from the center, as shown in Figure 1 (a).

Consider the function $\psi(w) = (w - w_0)^{1/m}$. Which first takes the disk to the origin $(w - w_0)$ and then applies the $n$-th root which has the effect of creating $m$ regions on a disk of radius $\delta^{1/m}$, which we depict in Figure 1 (b).

Then to obtain $z$ by applying $\xi^{-1}$, which is a bijection and conformal, so it will preserve the regions and the angles, but might not preserve overall shapes, as shown in Figure X (c).

See caption. — Figure 1. Visualization of the inverse of a non-constant function $f(z)$ applied to a small disk. (a) Here we trace what happens with the red segment on the $w$-plane. (b) The function $(w - w_0)^{1/m}$ maps the disk into $m$ "slices" of a disk at the origin (in the drawing we assume $m = 3$). (c) The function $\xi^{-1}$ is a bijection and conformal, so there should be a 1:1 correspondence between the red segments, and locally the angles should be preserved.

Conclusion

The open map theorem is simple to state but non-trivial to prove. It relies on several concepts and results from previous posts, namely zeros and winding numbers.

It took me quite a while to go through this section of Ahlfors’s book, especially the “visualization” of Lemma 9. It helped to study multi-valued functions first [8].

Appendix

Lemma 10. Let $f(z)$ be a holomorphic function in $\Omega$ and $z_1, z_2, \cdots, z_n$ be its zeros, and $m_1, m_2, \cdots, m_n$ their order. Let $\gamma$ be a closed curve in $\Omega$ and $n(\gamma, a)$ the winding number of a point $a$.

Then:

\[(5) \quad \sum_{i = 1}^n n(\gamma, z_i) m_i = \frac{1}{2\pi i} \int_{\gamma} \frac{f'(z)}{f(z)}dz\] First we apply the logarithm to $(1)$ we get: $$\ln f(z) = m_1 \ln (z - z_1) + m_2 \ln (z - z_2) + \cdots + m_n \ln (z - z_n) + \ln g(z)$$ Differentiating: $$\frac{d \ln f(z)}{dx} = \frac{m_1}{z - z_1} + \frac{m_2}{z - z_2} + \cdots + \frac{m_n}{z - z_n} + \frac{d \ln g(z)}{dz}$$ We can use the logarithmic derivative identity: $$ \frac{d \ln f(z)}{dz} = \frac{f'(z)}{f(z)} $$ for both $f(z)$ and $g(z)$ to obtain: $$ \frac{f'(z)}{f(z)} = \paren{\sum_{i = 1}^n \frac{m_i}{z - z_i}} + \frac{g'(z)}{g(z)} $$ We integrate this expression over the curve $\gamma$: $$ (2.1) \quad \int_\gamma \frac{f'(z)}{f(z)} dz = \int_\gamma \paren{\sum_{i = 1}^n \frac{m_i}{z - z_i}}dz + \int_\gamma \frac{g'(z)}{g(z)}dz $$ Since $g'(z)$ is holomorphic and $g(z) \ne 0$ from Lemma 1, then $g'(z)/g(z)$ is holomorphic and from Cauchy's Integral Theorem [4] we have that $$\int_\gamma \frac{g'(z)}{g(z)}dz = 0$$ Swaping the sum and integral in $(2.1)$ gives us: $$ \int_\gamma \frac{f'(z)}{f(z)} dz =\sum_{i = 1}^n \int_\gamma \frac{m_i}{z - z_i}dz $$ Moving the constant $m_i$ out of the integral and dividing by $2\pi i$: $$ \frac{1}{2\pi i} \int_\gamma \frac{f'(z)}{f(z)} dz =\sum_{i = 1}^n \frac{m_i}{2\pi i} \int_\gamma \frac{1}{z - z_i}dz $$ Using the definition of winding number $$n(\gamma, a) = \frac{1}{2\pi i} \int_\gamma \frac{1}{z - a}dz$$ we obtain: $$ \frac{1}{2\pi i} \int_\gamma \frac{f'(z)}{f(z)} dz =\sum_{i = 1}^n n(\gamma, z_i) m_i $$ QED

References

[1] Complex Analysis - Lars V. Ahlfors
[2] NP-Incompleteness: Holomorphic Functions are Analytic
[3] Cauchy’s Integral Formula
[4] NP-Incompleteness: Cauchy Integral Theorem
[5] NP-Incompleteness: The Winding Number
[6] NP-Incompleteness: Holomorphic Functions
[7] NP-Incompleteness: Conformal Maps
[8] NP-Incompleteness: Multi-valued functions

| Tags: analysis