kuniga.me > NP-Incompleteness > Cross Ratio

Cross Ratio

13 Jan 2024

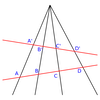
In this post we’ll discuss the concept of the cross-ratio which has its origins in geometry, but we’ll mainly consider it in the context of complex analysis.

This is the 4rd post in the series of my study notes on complex analysis. I recommend first checking the previous posts:

1. Holomorphic Functions
2. Conformal Maps
3. Möbius Transformation

Definition

In $\mathbb{R}^2$, let $A, B, C$ and $D$ be four collinear points where at least 3 of them are distinct. We define the cross-ratio between them as:

\[(A, B, C, D) = \frac{\overline{AC} \cdot \overline{BD}}{\overline{BC} \cdot \overline{AD}}\]

The notation $\overline{AC}$ represents the distance between $A$ and $C$. However, we assume the line where these points has a direction so the distance has a sign. We can assume it’s positive if $A$ appears before $C$ and negative otherwise. The convention doesn’t matter as long as it’s consistent.

So the cross ratio is a function taking 4 numbers in $\mathbb{R}^2$ and returning a real number. This concept is important because the cross ratio is preserved under linear fractional transformations (Möbius transformations) such as translation, rotation and homothety.

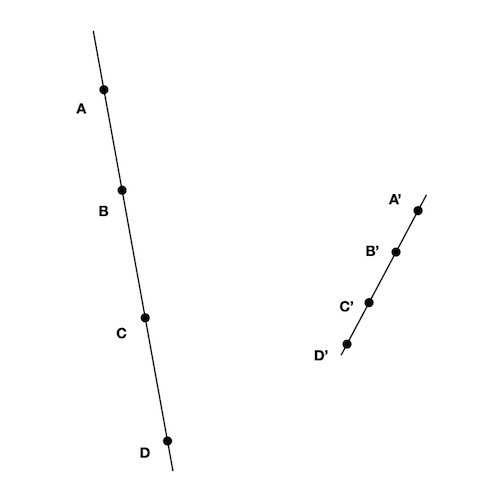
For example, in Figure 1, assuming the line containing $A, B, C$ and $D$ was transformed into the one $A’, B’, C’$ and $D’$ using linear fractional transformations, then we have

\[(A, B, C, D) = (A', B', C', D')\]

This might be useful for example when we know points $A, B, C$ and $D$ and between $A’, B’$ and $C’$ and we want to find $D’$. One example is calculating actual distances from projections: suppose we have a photograph from a given perspective (a projection) from which we can measure the distance of 4 collinear points. We also have the actual coordinates for 3 reference points.

We can find the 4th via the cross-ratio. Federico Ardila provides a very interesting example in a Numberphile video [3].

Complex Plane

We now generalize the cross-ratio for the complex plane. Instead of $\mathbb{R}^2$ the function takes in 4 complex numbers and also returns a complex number. Let $z_1, z_2, z_3$ be 3 distinct points on the extended complex plane. The function given by

\[(1) \quad f(z) = \frac{(z - z_3)}{(z - z_4)} \cdot \frac{(z_2 - z_4)}{(z_2 - z_3)}\]

It has the property of $f(z_2) = 1$, $f(z_3) = 0$ and $f(z_4) = \infty$ which we can verify by simple algebraic manipulation. It turns out the cross-ratio is a special type of Möbius transformation:

Theorem 1. The cross ratio is a Möbius transformation.

Recall that the Möbius transformation has the following form: $$S(z) = \frac{az + b}{cz + d}$$ We set $a = (z - z_3)$, $b = -z_2(z - z_3)$, $c = (z - z_2)$ and $d = -z_3(z_1 - z_2)$ and verify that replacing these in $(1)$ leads to $(1)$. It remains to show that $ad - bc \ne 0$: $$ad - bc = -(z_1 - z_3)z_3(z_1 - z_2) + z_2(z_1 - z_3)(z_1 - z_2) = (z_1 - z_2)(z_1 - z3)(z_2 - z_3)$$ Since the points are all distinct, by definition, we conclude our proof.

Theorem 2 is a fundamental property which makes cross-ratio useful - that it is invariant under a Möbius transformation:

Theorem 2. Let $f(z)$ be a Möbius transformation and $(z_1, z_2, z_3, z_4)$ a given cross ratio. Then $(z_1, z_2, z_3, z_4) = (f(z_1), f(z_2), f(z_3), f(z_4))$.

This can be verified by simple algebraic manipulation. First we write $(f(z_1), f(z_2), f(z_3), f(z_4))$ as a cross-ratio $(1)$: $$(2.1) \quad \frac{(f(z_1) - f(z_3))}{(f(z_1) - f(z_4))} \cdot \frac{(f(z_2) - f(z_4))}{(f(z_2) - f(z_3))}$$ For any distinct $z_a$ and $z_b$ let's define $g(z_a, z_b) = f(z_a) - f(z_b)$. Since $f(z)$ is a Möbius transformation, we can write $f(z)$ as: $$f(z) = \frac{az + b}{cz + d}$$ So $g(z_a, z_b)$ can be expanded to: $$g(z_a, z_b) = f(z_a) - f(z_b) = \frac{az_a + b}{cz_a + d} - \frac{az_b + b}{cz_b + d}$$ Normalizing the denominator: $$= \frac{(az_a + b)(cz_b + d) - (az_b + b)(cz_a + d)}{(cz_a + d)(cz_b + d)}$$ Distributing terms on the numerator: $$= \frac{acz_az_b + az_ad + bcz_b + bd - acz_az_b - az_bd - bcz_a - bd}{(cz_a + d)(cz_b + d)}$$ Canceling the terms: $$= \frac{az_ad + bcz_b - az_bd - bcz_a}{(cz_a + d)(cz_b + d)}$$ Refactoring and isolating the independent factor: $$(2.2) \quad g(z_a, z_b) = (ad - bc) \frac{(z_a - z_b)}{(cz_a + d)(cz_b + d)}$$ We can use the $g(z_a, z_b)$ notation in (2.1) and get: $$\frac{g(z_1, z_3)}{g(z_1, z_4)} \cdot \frac{g(z_2, z_4)}{g(z_2, z_3)}$$ If we replace $(2.2)$ in the equation above, we can already eliminate the factor $(ad - bc)$ in $g(z_a, z_b)$ since it's common across all terms, and obtain: $$\frac{(z_1 - z_3)(cz_1 + d)(cz_4 + d)}{(z_1 - z_4)(cz_1 + d)(cz_3 + d)} \cdot \frac{(z_2 - z_4)(cz_2 + d)(cz_3 + d)}{(z_2 - z_3)(cz_2 + d)(cz_4 + d)}$$ Cancelling the common factors: $$\frac{(z_1 - z_3)}{(z_1 - z_4)} \cdot \frac{(z_2 - z_4)}{(z_2 - z_3)}$$ which is exactly the cross ratio $(z_1, z_2, z_3, z_4)$.

Finally, we can make a connection with circles and lines from the previous section:

Theorem 3. The cross ratio $(z_1, z_2, z_3, z_4)$ is real if and only if these four points lie on a circle or on a line.

First let's prove that if the four points line on a circle or line then the cross ratio is real.

Let's define the function $f(z) = (z, z_2, z_3, z_4)$, where $z$ belongs to a line or a circle. Since it's a cross ratio, we know that $f(z_2) = 1$, $f(z_3) = 0$ and $f(z_4) = \infty$, so they all lie on the $x$-axis.

By Theorem 1 $f(z)$ is a Möbius transformation and we can use Corollary 9 in [2] from to show that $f(z)$ maps circles and lines to either circles or lines. But since we have 3 collinear points in the image of $f$, it cannot be a circle, so it has to be a line and this line must be the $x$-axis, since 2 distinct points uniquely determine a line.

So we conclude that $f(z)$ is real for any $z$.

Now we show that if the image of the cross ratio is real, the corresponding points $z_1, z_2, z_3$ and $z_4$ lie on a line or a circle. Since $f$ is a Möbius transformation, by Theorem 1 in [2], the inverse $f^{-1}(w)$ exists, and in here $w \in \mathbb{R}$. By Corollary 9 in [2] again, we conclude that the image of $f^{-1}(w)$ lies on a line or a cicle. In particular we have $z_2 = f^{-1}(1)$, $z_3 = f^{-1}(0)$ and $z_3 = f^{-1}(\infty)$, and there is $w^{*} = f(z_1) \in \mathbb{R}$ such that $z_1 = f^{-1}(w^{*})$.

Taking the conjugate of a complex number is not a Möbius transformation, however, we can show that the cross ratio is invariant with the conjugate operation as well:

Theorem 4. Let $(z_1, z_2, z_3, z_4)$ be a cross ratio. Then

\[\overline{(z_1, z_2, z_3, z_4)} = (\overline{z_1}, \overline{z_2}, \overline{z_3}, \overline{z_4})\] We can prove this by simple arithmetic identities for conjugate numbers. We have: $$\overline{\left(\frac{z_1 - z_3}{z_1 - z_4} \cdot \frac{z_2 - z_4}{z_2 - z_3}\right)}$$ Since conjugate is invariant with subtration, multiplication and division, we'll get $$\frac{(\overline{z_1} - \overline{z_3})}{(\overline{z_1} - \overline{z_4})} \cdot \frac{(\overline{z_2} - \overline{z_4})}{(\overline{z_2} - \overline{z_3})}$$ Which is the definition of $(\overline{z_1}, \overline{z_2}, \overline{z_3}, \overline{z_4})$.

Conclusion

In this post we learned about a special type of Möbius transformation, known as the cross-ratio. It originates from classical Euclidean geometry in the study of perspectives but was later extended to the projective (non-Euclidean) geometry. Projective geometry has a natural correspondence with the extended complex numbers.

I had a hard time grokking the concept of cross-ratio and how it can be used, but Ardila’s video [3] was illuminating.

References

• [1] Complex Analysis - Lars V. Ahlfors
• [2] NP-Incompleteness - Möbius Transformation
• [3] Youtube - The Cross Ratio - Numberphile