Möbius Transformation

kuniga.me > NP-Incompleteness > Möbius Transformation

Möbius Transformation

08 Jan 2024

a bunch of lines and circles abstract art

In this post we’ll discuss the Möbius transformation, which is relatively simple but which is versatile enough that a lot of useful transformations can be done through it.



This is the 3rd post in the series of my study notes on complex analysis. I recommend first checking the previous posts:

  1. Holomorphic Functions
  2. Conformal Maps

Definition

We define a Möbius transformation as a function $S: \mathbb{C} \rightarrow \mathbb{C}$ as:

\[(1) \qquad w = S(z) = \frac{az + b}{cz + d}\]

For $a, b, c, d \in \mathbb{C}$ and with $ad - bc \ne 0$. Wikipedia [3] suggests that Möbius transform refers to a different concept, so we must be careful in not treating transformation and transform as synonyms.

Inverse

Theorem 1. the inverse of a Möbius transformation is

\[z = S^{-1}(w) = \frac{dw - b}{-cw + a}\]

and is also a Möbius transformation.

Let's first show that $S^{-1}(S(z)) = z$ $$= \frac{d(az + b)/(cz + d) - b}{-c(az + b)/(cz + d) + a}$$ Multiplying both numerator and denominator by $(cz + d)$: $$= \frac{d(az + b) - b(cz + d)}{-c(az + b) + a(cz + d)}$$ Distributing terms: $$= \frac{adz + bd - bcz - bd}{-acz - bc + acz + ad}$$ Cancelling terms: $$= \frac{adz - bcz}{-bc + ad}$$ Isolating $z$: $$= \frac{z(ad - bc)}{ad - bc} = z$$ To show $S^{-1}(w)$ is a Möbius transformation of the form $$(2) \qquad w = S'(z) = \frac{a'z + b'}{c'z + d'}$$ We need that $a'd' - b'c' = 0$. For $S^{-1}$ we have $a' = d, b' = -d, c' = -c$ and $d' = a$, which gives us $da - (-b)(-c) = ad - bc$. Which is non-zero assuming the original $S$ is a Möbius transformation.

Infinity

If we consider the extended complex plane [5], we can define the special values $S(\infty) = a/c$ and $S(-d/c) = \infty$.

Normalized

We say the Möbius transformation is normalized if $ad - bc = 1$. Every transformation has exactly two normalized forms, given $ad - bc = (-a)(-d) - (-b)(-c)$.

Properties

Composition

Theorem 2 shows that the composition of Möbius transforms is also a Möbius transform.

Theorem 2. Let $S_1$ and $S_2$ be Möbius transforms. Then $S_2 \circ S_1$ is also a Möbius transform.

This is a simple proof, but requires some tedious algebraic manipulation. First we use $C$ for $S_1$ and $S_2$: $$S_1(z) = \frac{a_1z + b_1}{c_1z + d_1}, \qquad S_2(z) = \frac{a_2z + b_2}{c_2z + d_2}$$ So $S(z) = S_2(S_1(z))$ is $$ S(z) = \frac{a_2 (a_1z + b_1)/(c_1z + d_1) + b_2}{c_2 (a_1z + b_1) / (c_1z + d_1) + d_2} $$ Multiplying both numerator and denominator by $(c_1z + d_1)$: $$ = \frac{a_2 (a_1z + b_1) + b_2(c_1z + d_1)}{c_2 (a_1z + b_1) + d_2(c_1z + d_1)} $$ Distributing: $$ = \frac{a_1a_2z + a_2b_1 + b_2c_1z + b_2d_1}{a_1c_2z + b_1c_2 + c_1d_2z + d_1d_2} $$ Isolating $z$: $$ = \frac{(a_1a_2 + b_2c_1)z + a_2b_1 + b_2d_1}{(a_1c_2 + c_1d_2)z + b_1c_2 + d_1d_2} $$ We can set $a = a_1a_2 + b_2c_1$, $b = a_2b_1 + b_2d_1$, $c = a_1c_2 + c_1d_2$ and $d = b_1c_2 + d_1d_2$. It remains to show that $ad - bc \ne 0$. This is $$= (a_1a_2 + b_2c_1)(b_1c_2 + d_1d_2) - (a_2b_1 + b_2d_1)(a_1c_2 + c_1d_2)$$ Distributing: $$= a_1a_2b_1c_2 + a_1a_2d_1d_2 + b_1b_2c_1c_2 + b_2c_1d_1d_2 - \\ a_1a_2b_1c_2 - a_2b_1c_1d_2 - a_1b_2c_2d_1 - b_2c_1d_1d_2$$ Cancelling terms: $$= a_1a_2d_1d_2 + b_1b_2c_1c_2 - a_2b_1c_1d_2 - a_1b_2c_2d_1$$ Grouping by $a_1d_1$ and $b_1c_1$: $$ = a_1d_1(a_2d_2 - b_2c_2) - b_1c_1(a_2d_2 - b_2c_2)$$ Grouping by $(a_2d_2 - b_2c_2)$: $$= (a_1d_1 - b_1c_1)(a_2d_2 - b_2c_2)$$ Since both factors are non-zero by definition, their product must be non-zero, so $ad - bc \ne 0$.

Conformal Maps

At we mentioned in the beginning:

Theorem 3. The Möbius transformation is a conformal map.

The idea is to show that a Möbius transformation is a holomorphic function with a non-zero derivative and then use Theorem 3 in [2] to show it's a conformal map.

First we consider the derivative of $(1)$. If we define the intermediary functions $g(z) = az + b$ and $h(z) = cz + d$, we can use the quotient rule for derivatives: $$f'(z) = \frac{g'(z)h(z) - g(z)h'(z)}{h(z)^2} = \frac{(acz + ad) - (acz + bc)}{(cz + d)^2} = \frac{ad - bc}{(cz + d)^2}$$ By definition of Möbius transformation $ad - bc \ne 0$. If $z \ne -d/c$, $f'(z)$ exists and it's non 0, so we can use Theorem 3 in [2] to conclude it's a conformal map.

Matricial form

We can represent a Möbius transformation $S$ in matricial form. First, let’s define $z_1, z_2, w_1, w_2$ as:

\[(3) \quad \begin{align} w_1 &= a z_1 + b z_2 \\ w_2 &= c z_1 + d z_2 \\ \end{align}\]

And $a, b, c$ and $d$ from $S$ $(1)$. We can define a Möbius from these two equations, as stated by Lemma 4:

Lemma 4. If $z = z_1 / z_2$ then $S(z) = w_1 / w_2$.

We'll get $$w = \frac{w_1}{w_2} = \frac{a z_1 + b z_2}{c z_1 + d z_2}$$ Replacing $z_1 = z z_2$, $$= \frac{w_1}{w_2} = \frac{a z z_2 + b z_2}{c z z_2 + d z_2}$$ If we cancel out the common $z_2$ factor we obtain $(1)$. We can represent the equations as a matrix multiplication:

Equations $(3)$ can be written in matricial form:

\[\begin{pmatrix} w_1 \\ w_2 \end{pmatrix} = \begin{pmatrix} a & b\\ c & d \end{pmatrix} \begin{pmatrix} z_1\\ z_2 \end{pmatrix}\]

This is convenient because composing Möbius transformations correspond to matrix multiplication.

There are 3 special matrices we shall consider.

Translation

The matrix:

\[\begin{pmatrix} 1 & \alpha \\ 0 & 1 \end{pmatrix}\]

results in $w_1 = z_1 + \alpha z_2$ and $w_2 = z_2$, so

\[w = \frac{w_1}{w_2} = \frac{z_1 + \alpha z_2}{z_2} = \alpha + \frac{z_1}{z_2} = z + \alpha\]

If we consider $z$ as a point in the complex plan, this corresponds to a translation, so this transform is known as the parallel translation.

Rotation and homothety

The matrix:

\[\begin{pmatrix} k & 0 \\ 0 & 1 \end{pmatrix}\]

results in $w_1 = k z_1$ and $w_2 = z_2$, so $w = kz$. If $\abs{k} = 1$, then it’s called a rotation. To see why, we can consider the numbers in polar form $\abs{w} e^{\theta_w} = \abs{k} e^{\theta_k} \abs{z} e^{\theta_z}$. Since $\abs{k} = 1$ we have $\abs{w} =\abs{z}$ and $\theta_w = \theta_z + \theta_k$, so if we consider the vectors defined by $z$ and $w$ in the complex plane, $w$ corresponds to a rotation of $z$ by $\theta_k$ around the origin.

If $k$ is a positive real, we have a homothety (homo = same, theta = angle) or dilation, which corresponds to scaling the distance of a point $z$ to the origin without changing the direction. We mentioned this as an example of a conformal map in [2].

For arbitrary complex $k$ we can obtain the corresponding transformation via a homothety by $\abs{k}$ followed by a rotation by $k/\abs{k}$ since $k = \abs{k} k/\abs{k}$.

Inversion

The matrix:

\[\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\]

results in $w_1 = z_2$ and $w_2 = z_1$, so $w = 1/z$ and hence is called a inversion.

Turn out all we need are these 4 types of matrix to compose any Möbius transformation, as stated by Theorem 5:

Theorem 5. Any Möbius transformation can be obtained via a composition of parallel translation, rotation, homothety and inversion.

Let's conside 2 cases: Case 1 where $c \ne 0$, then we can rewrite $(1)$ as: $$(5.1) \quad \frac{az + b}{cz + d} = \frac{bc - ad}{c^2 (z + d/c)} + \frac{a}{c}$$ We can achieve any Möbius transformation by first translating with $\alpha = d/c$: $$z + d/c$$ followed by an inversion: $$\frac{1}{z + d/c}$$ we can then use a homothety followed by a rotation to multiply by $k = (bc - ad) /c^2$: $$\frac{bc - ad}{c^2 (z + d/c)}$$ Finally we do another translation with $\alpha = a/c$ to obtain $(5.1)$. Case 2: If $c = 0$, then we do a translation with $\alpha = b/a$ then a homothety + a rotation for $k = a/d$ to obtain: $$\left(z + \frac{b}{a}\right)\frac{a}{d} = \frac{az + b}{d}$$

Fixed Points and Normal Form

For a given Möbius transformation, a fixed point is a value $z$ such that $z = S(z)$, that is, a point for which $S$ transforms it into itself. Replacing in $(1)$ gives us

\[(4) \quad z = \frac{az + b}{cz + d}\]

If $c = 0$, then we have a linear equation and the fixed point is

\[z = \frac{b}{d - a}\]

We also have that $z = \infty$ is a fixed point in the extended complex plan since:

\[\lim_{z \rightarrow \infty} z = \lim_{z \rightarrow \infty} \frac{az + b}{d}\]

If $c \ne 0$, then we can write $(4)$ in the polynomial form:

\[\quad cz^2 + (d - a)z - b = 0\]

and we can find the fixed points $\gamma_1$ and $\gamma_2$ via the quadratic formula. It’s possible that $\gamma_1 = \gamma_2$ in which case the transformation has only one fixed point.

Let $f(z)$ be any Möbius transformation with two distinct fixed points $\gamma_1 \neq \gamma_2$. Let’s consider the function $g(z)$:

\[g(z) = \frac{z - \gamma_1}{z - \gamma_2}\]

Which is a Möbius transformation with $a=1, b=-\gamma_1, c=1$ and $d=-\gamma_2$.

We have that $g(\gamma_1) = 0$ and $g(\gamma_2) = \infty$. Conversely, since Möbius transformations have an inverse (Theorem 1), we have $g^{-1}(0) = \gamma_1$ and $g^{-1}(\infty) = \gamma_2$.

Now consider the composite function $g(f(g^{-1}(w)))$ or in simpler notation $gfg^{-1}(w)$. By Theorem 2 we know this is also a Möbius transformation. Let’s evaluate this function for $0$ and $\infty$.

We have that $g^{-1}(0) = \gamma_1$ and thus $fg^{-1}(0) = \gamma_1$ (since $\gamma_1$ is a fixed point of $f$), and finally $gfg^{-1}(0) = 0$. Throught a similar process we can reach the conclusion that $gfg^{-1}(\infty) = \infty$. We conlude that $0$ and $\infty$ are fixed points of $gfg^{-1}(w)$.

Let us denote $U = gfg^{-1}$. What does it look like? We can plug $U(0) = 0$ in $(1)$ to get $0 = b/d$ and conclude that $b = 0$. So we now have:

\[U(w) = \frac{aw}{cw + d}\]

For $w \ne 0$, we can divide both numerator by $w$:

\[U(w) = \frac{a}{c + d/w}\]

And consider the inverse of $U(w)$:

\[\frac{1}{U(w)} = \frac{c + d/w}{a}\]

Using the fact that $U(\infty) = \infty$, we obtain $0 = c / a$, so it must be that $c = 0$. Thus, $U(w)$ has the form:

\[U(w) = \frac{a}{d} w\]

Given that $a/d$ is a complex number, we can consider its polar form, say $r e^{i\theta}$, so that $U(w) = r e^{i\theta} w$. In other words, $U(w)$ is a simple transformation involving only a homothety by $r$ and rotation by $\theta$ on the transformed space $w$.

So we have: $g(f(g^{-1}(w))) = r e^{i\theta} w$. Let $z = g^{-1}(w)$, so that $w = g(z)$. We can write the previous equation as $g(f(z)) = r e^{i\theta} g(z)$, so we don’t need to work with the inverse of $g$. Replacing the definition of $g(z)$ we get:

\[\frac{f(z) - \gamma_1}{f(z) - \gamma_2} = r e^{i\theta} \frac{z - \gamma_1}{z - \gamma_2}\]

This is known as the normal form of a Möbius transformation. The term “normal” refers to the normalization that happens when we transform the original domain and image of $f(z)$ through $g(z)$ so that the equivalent Möbius transformation becames much simpler.

A similar analysis can be done for a single fixed point (i.e. when $\gamma_1 = \gamma_2$) but we’ll not cover them here.

Transforming Circles and Lines

Let’s consider what happens when we apply a Möbius transformation $S$ to a line and a circle (in the complex plane). Let’s start with the line and skip inversion for now. Intuitively translating a line, rotating it and scaling it should preserve its form. That’s what Lemma 6 shows more formally.

Lemma 6 The parallel translation, rotation and homothety transformations map lines to lines

A line in the complex plane is defined by $z = z_0 + t v$ for some $z_0, v \in \mathbb{C}$ and $t \in \mathbb{R}$. If we translate by $\alpha$, we have $w = z + \alpha = (z_0 + \alpha) + t v$. Since $(z_0 + \alpha)$ is a complex number, $w$ forms a line. Suppose we rotate $z$ by some $\phi$. First consider $z$ in polar form: $$\abs{z}e^{i\theta_z} = \abs{z_0}e^{i\theta_{z_0}} + t \abs{v}e^{i\theta_{v}}$$ Rotating $z$ about the origin by $\phi$ is equivalent to multiply it by $e^{i \phi}$, so $$w = \abs{z}e^{i(\theta_z + \phi)} = \abs{z_0}e^{i(\theta_{z_0} + \phi)} + t \abs{v}e^{i(\theta_{v} + \phi)}$$ So we basically rotated $z_0$ and $v$ by $\phi$ about the origin but they're still complex numbers, so $w$ is on a line. Multiplying $z$ by a positive scalar leads to a similar conclusion.

Let’s continue with the circle and still skip inversion. Intuitively too translating a circle, rotating it about the origin and scaling it should preserve its form. That’s what Lemma 7 shows more formally.

Lemma 7 The parallel translation, rotation and homothety transformations map circles to circles

It's convenient to define a point in a circle of radius $r$ centered in $z_0$ by $z = z_0 + r e^{i\theta}$, where $z_0 \in \mathbb{C}$, $r \in \mathbb{R}$ and $0 \le \theta \lt 2\pi$. Translating by $\alpha$ gives us a circle with center $z_0 + \alpha$, rotating about the origin consists in multiplying by $e^{i\phi}$, so we get: $$w = z_0 e^{i\phi} + r e^{i(\theta + \phi)}$$ which is a circle with center $z_0 e^{i\phi}$ ($z_0$ rotated about the origin). Since $e$ has period $2\pi$, adding a constant to $0 \le \theta \lt 2\pi$ doesn't change the final result. Finally, multiplying by a scalar $k$ gives us $$w = k z_0 + (kr) e^{i\theta}$$ a cicle with center $k z_0$ and radius $kr$.

The hardest transformation is the inversion $1/z$, which can map circles into lines and vice-versa, so we treat them on the same lemma, Lemma 8:

Lema 8. The inversion transformation maps circles to circles or lines, and lines to circles.

The first part of the proof consists in showing that circles are mapped to either circles or lines. This time it's more convenient to represent a circle with center $z_0$ and radius $r$ as $$\abs{z - z_0} = r$$ Squaring and using the identity $c \overline{c} = \abs{c}^2$ and that $\overline{c - d} = \overline{c} - \overline{d}$ [3]: $$(8.1) \quad \abs{z - z_0}^2 = (z - z_0)\overline{(z - z_0)} = (z - z_0)(\overline{z} - \overline{z_0}) = r^2$$ Let $w = 1/z$ be the transformed value of $z$. Thus $z = 1/w$ and since conjugate of the inverse is the inverse of the conjugate: $\overline{z} = 1/{\overline{w}}$. Replacing in $(8.1)$: $$\left(\frac{1}{w} - z_0\right)\left(\frac{1}{\overline{w}} - \overline{z_0}\right) = r^2$$ Distributing: $$\frac{1}{w\overline{w}} - \frac{\overline{z_0}}{w} - \frac{z_0}{\overline{w}} + z_0\overline{z_0} = r^2$$ Multiplying by $w\overline{w}$, using $z_0\overline{z_0} = \abs{z_0}^2$ and isolating $1$: $$(8.2) \quad 1 = \overline{z_0}\overline{w} + z_0w + (r^2 - \abs{z_0}^2) w\overline{w}$$ We now split into two cases. Case 1: $r \neq \abs{z_0}$. This hypothesis enables us to replace $1$ with $(r^2 - \abs{z_0}^2)/(r^2 - \abs{z_0}^2)$ (this is a trick to allow some factoring later): $$\frac{r^2 - \abs{z_0}^2}{r^2 - \abs{z_0}^2} = \overline{z_0}\overline{w} + z_0w + (r^2 - \abs{z_0}^2) w\overline{w}$$ We add $\abs{z_0}^2/(r^2 - \abs{z_0}^2)$ to both sides: $$\frac{r^2}{r^2 - \abs{z_0}^2} = \overline{z_0}\overline{w} + z_0w + (r^2 - \abs{z_0}^2) w\overline{w} + \frac{\abs{z_0}^2}{r^2 - \abs{z_0}^2}$$ And then rename $(r^2 - \abs{z_0}^2)$ as $\rho$ for simplicity of notation: $$\frac{r^2}{\rho} = \overline{z_0}\overline{w} + z_0w + \rho w\overline{w} + \frac{\abs{z_0}^2}{\rho}$$ Dividing by $\rho$: $$\frac{r^2}{\rho^2} = \frac{\overline{z_0}\overline{w}}{\rho} + \frac{z_0w}{\rho} + w\overline{w} + \frac{\abs{z_0}^2}{\rho^2}$$ The right hand side can be refactored as: $$\frac{r^2}{\rho^2} = \left(w + \frac{\overline{z_0}}{\rho}\right) \left(\overline{w} + \frac{z_0}{\rho}\right) = \left(w + \frac{\overline{z_0}}{\rho}\right) \left(\overline{w + \frac{\overline{z_0}}{\rho}}\right) = \left\lvert w + \frac{\overline{z_0}}{\rho} \right\rvert^2$$ Which is the equation of a circle: $$\left\lvert w + \frac{\overline{z_0}}{\rho} \right\rvert = \left\lvert \frac{r}{\rho} \right\rvert$$ Replacing back $\rho$, we have a circle with radius $$r' = \left\lvert \frac{r}{r^2 - \abs{z_0}^2} \right\rvert$$ and center $$w_0 = -\frac{\overline{z_0}}{r^2 - \abs{z_0}^2} = \frac{\overline{z_0}}{\abs{z_0}^2 - r^2}$$ Now we consider Case 2: $r = \abs{z_0}$. This is when the origin is contained in the original circle $\abs{z - z_0} = r$. In this case equation $(8.2)$ becomes: $$1 = \overline{z_0}\overline{w} + z_0w$$ We can expand these complex numbers into their real and imaginary parts, $z_0 = x_0 + i y_0$ and $w = w_x + i w_y$: $$= (x_0 - i y_0)(w_x - i w_y) + (x_0 + i y_0)( w_x + i w_y)$$ Multiplying factors: $$= x_0w_x -i x_0w_y - i y_0w_x - y_0w_y + x_0w_x + i x_0w_y + i y_0w_x - y_0w_y$$ Cancelling factors: $$(8.3) \quad 2x_0w_x -2 y_0w_y = 1$$ Since $(x_0, y_0)$ is constant, the above satisfies $\alpha w_x + \beta w_y = 1$ for fixed reals $\alpha$ and $\beta$, which is the equation of a line. Thus $w$ defines a line in the complex plane.

We now continue to the second part. Since every line can be represented via $\alpha w_x + \beta w_y = 1$, then for each line there's exactly one circle that maps into it. More specifically, by using $(8.3)$ we find it's one with center $x_0 = \alpha/2$ and $y_0 = -\beta/2$ and radius $r = \abs{z_0} = \sqrt{\alpha^2 + \beta^2}/2$.

The inverse of $w = f(z) = 1/z$ is $f^{-1}(w) = 1/w$, which is also an inversion, so if $w$ defines a line, $z$ defines a circle. Thus an inversion of form $1/z$ turns a line into a circle. QED.

Since any Möbius transformation is a “composition chain” of the basic transforms we’ve discussed, putting all these lemmas together we get the corollary:

Corollary 9: A Möbius transformation maps cicles/lines into circles/lines.

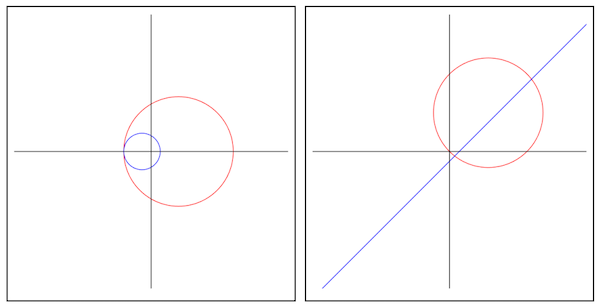
See caption.
Figure 1: (left) A circle of radius $r=2$ centered at $(1,0)$ transformed into a circle of radius $r=2/3$ at $(-1/3, 0)$. (right) A circle of radius $r=2$ centered at $(\sqrt{2}, \sqrt{2})$. Since we have $x_0^2 + y^2 = r^2$, the image degenerates to a line. Source: Observable

Conclusion

In this post we learned about a special type of conformal map, known as the Möbius transformation. In [1] Ahlfors calls them linear (fractional) transformations, since it’s a quotient of two linear functions.

References

Source code | RSS feed RSS Icon | Tags: analysis