kuniga.me > NP-Incompleteness > The Riemann Zeta Function

The Riemann Zeta Function

25 Oct 2025

Bernhard Riemann was a German mathematician. He initially planned to study theology at the University of Göttingen, but switched to mathematics on advice of Carl Friedrich Gauss.

Among Riemann’s contributions is a rigorous formulation of the integral operator, known as the Riemann integral. In complex analysis, he’s also known for the Riemann surfaces and in number theory, for the Riemann zeta function and the Riemann hypothesis with connections to the distribution of prime numbers.

In this post we’ll study the Riemann zeta function and briefly mention the Riemann hypothesis.

Dirichlet Series

In the post Basel problem, we learned that the infinite series

\[\sum_{n = 1}^\infty \frac{1}{n^2}\]

Is equal to $\pi^2 / 6$. How about for powers greater than $2$? Let’s generalize this series by parametrizing it on the exponent, denoting it as $\zeta(s)$:

\[\zeta(s) = \sum_{n = 1}^\infty \frac{1}{n^s}\]

To simplify the notation, henceforth we’ll assume that

\[\sum_{n} = \sum_{n = 1}^\infty\]

With this notation, $\zeta(1)$ is the non-convergent harmonic series and $\zeta(2)$ is the Basel problem above. We know that for $s \gt 1$ this series converges. However, for odd powers no closed formula is known, but for even powers Euler proved that:

\[\zeta(2k) = (-1)^{k+1} \frac{B_{2k}(2\pi)^{2k}}{2(2k)!}\]

Where $B_{2k}$ are the Bernoulli numbers of even indices, which can be computed in $O(2k)$. Fun fact: the Note G algorithm written by Ada’s Lovelace to compute Bernoulli numbers is regarded as the first algorithm created for computers (the Babbage machine). Bernoulli numbers of odd indices are always zero: $B_{2k + 1} = 0$. The first few Bernoulli numbers of even indices are: $B_0 = 1$, $B_2 = 1/6$, $B_4 = -1/30$.

If we use $k = 1$, we have:

\[\zeta(2) = \frac{B_2 (2\pi)^2}{2 2!} = \frac{\pi^2}{6}\]

For $k = 2$:

\[\zeta(4) = \frac{B_4 (2\pi)^4}{2 4!} = \frac{\pi^4}{90}\]

Now, what if we generalize to complex numbers? Then it becomes known as the Dirichlet Series. It’s possible to show that for $s \in \mathbb{R}$, $\zeta(s)$ converges if and only if $s > 1$.

For complex numbers we’ll denote $\sigma = \Re(s)$. The convergence is given by Lemma 1:

Lemma 1. $\zeta(s)$ converges if $\sigma \gt 1$.

We have that $\sigma = \Re{(s)}$ and that $\Re{(s)} \le \abs{s}$, so we have: $$ \abs{\sum_{n} n^{-\sigma}} \le \sum_{n} \abs{n^{-\sigma}} \le \sum_{n} n^{-\abs{s}} $$ So if $\sigma > 1$ then $\abs{s} > 1$ and the right most sum above is finite and so is the left most one.

Primes

We can connect the Dirichlet series to the prime numbers. In particular:

Theorem 2. If $\sigma > 1$ and $p_n$ the set of prime numbers with $p_1 = 2, p_2 = 3$, etc. Then,

\[\frac{1}{\zeta(s)} = \prod_{n} (1 - p_n^{-s})\] First we need to show that the product converges. Corollary 3 in [2] states that: Let $a_n$ be a (possibly infinite) set of complex numbers. Then the product: $$ P = \prod_{n} (a_n + 1) $$ converges absolutely if $$ \sum_{n} \abs{a_n} $$ converges. In our case, this means we just need to prove that $$ \sum_{n} \abs{p_n^s} $$ converges. We have that $\abs{p_n^s} = p_n^\sigma$. From Lemma 1 we know that $$ \sum_{n} n^\sigma $$ converges for $\sigma > 1$. Since the set of primes is a subset of the non-zero naturals, we conclude that $$ \sum_{n} p_n^\sigma $$ converges and so does the product for $\sigma > 1$. Now consider: $\zeta(s) (1 - 2^{-s})$: $$ \zeta(s) (1 - 2^{-s}) = \sum_n n^{-s} - \sum_n (2n)^{-s} = \sum_{m \mbox{ is odd}} m^{-s} $$ For $\zeta(s) (1 - 2^{-s}) (1 - 3^{-s})$: $$ = \sum_n n^{-s} - \sum_n (2n)^{-s} - \sum_n (3n)^{-s} + \sum_n (6n)^{-s} $$ The first sum includes all non-zero naturals. The second sum "removes" terms with factor 2 and the third those with factor Numbers with both factors, i.e. divisible by 6, are removed twice, but one is added back by the fourth sum.

It's possible to show this more rigorously but adding a factor $(1 - p_n^s)$ removes all naturals divisible by $p_n$. If we do it for all the primes, the only number left are those not divisible by any prime, which is only 1: $$ \zeta(s) \prod_{n} (1 - p_n^{-s}) = 1 $$ or $$ \frac{1}{\zeta(s)} = \prod_{n} (1 - p_n^{-s}) $$ QED

This is know as the Euler product.

Gamma Function

There’s a really neat formula combining the Dirichlet series and gamma functions, known as the Mellin Integral:

Theorem 3. Let $\Re(s) > 1$ then:

\[(1) \quad \zeta(s) \Gamma(s) = \int_{0}^{\infty} \frac{x^{s - 1}}{e^{x} - 1} dx\] We use a result from Gamma functions that says: $$ \Gamma(s) = \int_{0}^\infty \frac{x^{s-1}}{e^x} dx $$ for $\Re(s) \gt 0$. Then we define $y = nx$ so that $dy/dx = n$ and do a change of variable: $$ \Gamma(s) = \int_{0}^\infty \frac{(ny)^{s-1}}{e^{ny}} n dy = \int_{0}^\infty \frac{n^s y^{s-1}}{e^{ny}} dy $$ or $$ n^{-s} \Gamma(s) = \int_{0}^\infty \frac{y^{s - 1}}{e^{ny}} dy $$ Adding for all positive naturals $n$: $$ \sum_n n^{-s} \Gamma(s) = \sum_n \int_{0}^\infty \frac{y^{s - 1}}{e^{ny}} dy $$ Rearranging (without justification on why we can do it for the sum and integral): $$ \Gamma(s) \sum_n n^{-s} = \int_{0}^\infty y^{s - 1} \left(\sum_n \frac{1}{e^{ny}} \right) dy $$ The sum on the left side is $\zeta(s)$. The one on the left is a geometric series with factor $1/e^{ny}$ that converges if $1/e^{ny} \lt 1$. This is not true if $y = 0$, but in that case since $\Re(s) \gt 1$, $y^{s - 1} = 0$ and it cancels out the $1/e^{ny}$ factor so we can assume $y \ne 0$ inside the sum. This gives us: $$ \Gamma(s) \zeta(s) = \int_{0}^\infty \frac{y^{s - 1}}{e^y - 1} dy $$ QED.

The requirement that $\Re(s) > 1$ is because the integral only converges on these conditions. What if we chose a path other than the positive real line?

Hankel Contour

The Hankel contour is a curve depicted below:

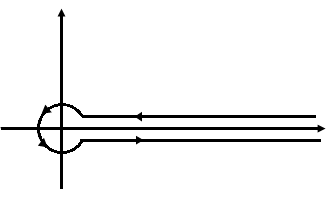
We can use $(1)$ to obtain a formula over the Hankel countour $C$ as stated by Theorem 4:

Theorem 4. Let $\Re(s) > 1$ then:

\[(2) \quad \zeta(s) = \frac{\Gamma(1 - s)}{2 \pi i} \int_{C} \frac{(-z)^{s - 1}}{e^z - 1} dz\] First we need to prove that $$ (4.1) \quad \int_{C} \frac{(-z)^{s - 1}}{e^z - 1} dz $$ is convergent. The observation is that for any fixed $s$, $e^z$ grows faster than $\abs{z}^{s}$, so since $\abs{z} \rightarrow \infty$ in $C$, the term tends to 0.

The requirement that the radius of $C$ be less than $2 \pi$ is not strictly required, but we must make sure $C$ does not contain the point $2 \pi i$ or any of its multiples because $e^{2\pi i} = 1$ and it would make the denominator of the fraction 0. The only other value of $z$ that makes $e^z = 1$ is $z = 0$, but we're already not including it.

This observation means that the fraction is holomorphic. This means that the integral over $C$ is path independent. We can then shrink shrink the circle of $C$ so that we end up with two parallel lines with opposite directions. This allows us to rewrite the integral $(4.1)$ over $x$ instead of $z$.

We must be very careful with this because $z^{s-1}$ is a multi-valued function. To see why we can write it as $z^{s-1} = e^{(s - 1) \log z}$ and the complex logarithm is a multi-valued function. This means we need to restrict the domain so guarantee this function is well defined. We do so by defining the negative x-axis as the branch cut. We can "avoid" crossing the branch cut by having $\arg z \in [-\pi, \pi]$. This choice is the principal branch of the complex logarithm, denoted by $\mbox{Log}(z) = \ln(\abs{z}) + i \arg(w)$. So we have: $$ z^{s-1} = e^{(s - 1) \mbox{Log } z} = e^{(s - 1) (\ln(\abs{z}) + i \arg(w))} = \abs{z}^{s-1} e^{(s - 1) i \arg(z)} $$ Since our original equation had $-z$ and now we're doing the analysis for $z$, we can assume some $w = -z$ and in this domain the Hankel curve is reversed: we have a line below the $x$-axis from $-\infty$ to $0$ and then above from $0$ to $-\infty$. For the line above the $x$-axis the argument tends to the constant $-\pi$, while for the line below the argument tends to the constant $\pi$. Let $w = x_w + i y_w$ with $y_w \rightarrow 0$. For the integral corresponding to the line above the $x$-axis we can write: $$ \int_{-\infty}^0 \frac{x_w^{s-1}}{e^{-x_w} - 1} dx_w = \int_{-\infty}^0 \frac{\abs{x_w}^{s-1} e^{- (s - 1) i \pi}}{ e^{-x_w} - 1} dx_w = - \int_{0}^{-\infty} \frac{\abs{x_w}^{s-1} e^{- (s - 1) i \pi}}{e^{-x_w} - 1} $$ Let $z = x + iy$, so we have $x = -x_w$. Replacing it back: $$ = - \int_{0}^{\infty} \frac{x^{s-1} e^{- (s - 1) i \pi}}{e^x - 1} dx $$ A similar reasoning for the line under the $x$-axis gives us: $$ = \int_{0}^{\infty} \frac{x^{s-1} e^{(s - 1) i \pi}}{e^x - 1} dx $$ Putting it all together: $$ \int_C \frac{(-z)^{s-1}}{e^z - 1} dz = - \int_{0}^{\infty} \frac{x^{s-1} e^{- (s - 1) i \pi}}{e^x - 1} + \int_{0}^{\infty} \frac{x^{s-1} e^{(s - 1) i \pi}}{e^x - 1} dx $$ Combine into one integral and extracing out the parts not dependent on $x$: $$ = (-e^{- (s - 1) i \pi} + e^{(s - 1) i \pi}) \int_{0}^{\infty} \frac{x^{s-1}}{e^x - 1} dx $$ The integral is $(1)$ if $\Re(s) > 1$. Let's analyze the term outside. Using the identity $\sin(z) = (e^{iz} - e^{-iz}) / 2i$: $$ -e^{- (s - 1) i \pi} + e^{(s - 1) i \pi} = 2 i \sin((s-1) \pi) $$ Using that $\sin((s - 1) \pi) = - \sin s\pi$ we can summarize: $$ \int_C \frac{(-z)^{s-1}}{e^z - 1} dz = -2 i \sin(s \pi) \Gamma(s) \zeta(s) $$ Now, using $\Gamma(s) \Gamma(1 - s) = \pi / (\sin (s \pi))$ or that: $$ \Gamma(s) \sin (s \pi) = \frac{\pi}{\Gamma(1 - s)} $$ we simplify further to: $$ \int_C \frac{(-z)^{s-1}}{e^z - 1} dz = \frac{-2 \pi i}{\Gamma(1 - s)} \zeta(s) $$ and finally rearranging terms: $$ \zeta(s) = \frac{-\Gamma(1 - s)}{2 \pi i} \int_C \frac{(-z)^{s-1}}{e^z - 1} dz $$

Now forget about Dirichlet series and just consider the function defined as $(2)$, which we happen to also call $\zeta(s)$. Theorem 5 shows this function is holomorphic for the any $s \ne 1$.

Theorem 5. The function

\[(3) \quad \zeta(s) = \frac{\Gamma(1 - s)}{2 \pi i} \int_{C} \frac{(-z)^{s - 1}}{e^z - 1}\]

is defined for $s \ne 1$.

This definition is what we call the Riemman Zeta function. For $\Re(s) \gt 1$ it happens to coincide with the Dirichlet series, but it’s a more general function, in the same way that the Gamma function is a more general version of the factorial, but they coincide for integer values.

Functional Equation

In the same way we can express the Gamma function recursively, i.e. $\Gamma(z + 1) = z \Gamma(z)$, we can do so for the zeta function, described by Theorem 6.

Theorem 6.

\[(2) \quad \zeta(s) = 2^s \pi^{s-1} \sin \left(\frac{\pi s}{2}\right) \Gamma(1 - s) \zeta(1 - s)\]

This formula is useful when $\Re(s) \lt 0$, because then $\Re(1 - s) \gt 1$ and we can more easily compute $\zeta(1 - s)$ (since it’s the Dirichlet series), than we can compute $\zeta(s)$. We’d still need to use $(3)$ for the interval $0 \le \Re(s) \lt 1$.

Zeros and Poles of the Riemman Zeta Function

Zeroes. What are the zeros of the zeta function? For $\Re(s) \gt 1$, the zeta function coincides with the Dirichlet series, which only has positive terms so it can’t add up to 0, so no zeros there.

Let’s assume $\Re(s) \lt 0$. In this case $\zeta(1 - s)$ cannot be 0 because it coincides with the Dirichlet series (case above). So the zeros must come from the remaining factors. Let’s define:

\[A(s) = 2^s \pi^{s-1} \sin \left(\frac{\pi s}{2}\right) \Gamma(1 - s)\]

So that $(2)$ becomes $\zeta(s) = A(s) \zeta(1 - s)$. The function $\sin(z)$ has zeros for $\pi n$, so assuming $z = \pi s / 2$, $\sin(\pi s / 2)$ has zeros for the even integers, $s = 0, \pm 2, \pm 4, \cdots$.

However, recall from [4] that the Gamma function $\Gamma(z)$ has the non-positive integers as poles, so assuming $z = 1 - s$, then $\Gamma(1 - s)$ has poles for $s$ as the positive integers. So the even poles will cancel out with the positive zeros of $\sin(\pi s / 2)$.

We’ll be left with the negative even zeros, which are now the zeros of $\zeta(s)$, which are called the trivial zeros. That is, $\zeta(s) = 0$ for $s = -2k$, $k \in \mathbb{N}$.

Lastly, we need to find the zeros in the strip $0 \le \Re(s) \le 1$. The Riemann Hypothesis state that all zeros in this strip, known as the non-trivial zeroes, have $\Re(s) = 1/2$.

Poles. We’ve cancelled out the even poles of $\Gamma(1 - s)$ but we’re still left with the odd poles. Suppose $s = 2k + 1$. Then $\zeta(1 - s)$ in $(2)$ becomes $\zeta(-2k)$. If $k > 0$, then $-2k$ is a trivial zero and thus $\zeta(1 - s)$ cancels out the odd poles. What remains is the only pole of the zeta function, $s = 1$.

Conclusion

It took me a while to realize that distinction between Dirichlet series and the zeta function. I thought the zeta function was the Dirichlet series but they only coincide for $\Re(s) > 1$.

I had read about the Riemann zeta function a long time ago, when I borrowed a book from my college’s library, The Music of the Primes and remembered being very interested in it.

I have a much more detailed understanding of the mathematics behind it and feel satisfied to have studied complex analysis for this.

References

• [1] Complex Analysis - Lars V. Ahlfors
• [2] NP-Incompleteness - Weierstrass
• [3] NP-Incompleteness - Harmonic Functions
• [4] NP-Incompleteness - The Gamma Function