kuniga.me > NP-Incompleteness > Runge's Theorem
Runge's Theorem
31 May 2025

Carl Runge was a German mathematician who, and among other things, is known for a result concerning the approximation of holomorphic functions. This result is know as the Runge’s approximation theorem and we’ll study its proof in this post.
Fun fact: Karl Weierstrass was one of Runge’s advisors.
Context
In the post Holomorphic Functions are Analytic [1] we saw that an holomorphic function can be written as a convergent series in a open circle.
More precisely, let $C$ be a circle centered in $a$ or radius $r$. If $f(z)$ is holomorphic in $\abs{z - a} \lt r$, then we can write it as a Taylor series:
\[f(z) = \sum_{n = 0}^{\infty} {c_n} (z - a)^n\]Then in Zeros and Poles we extended this idea to annular regions (i.e. a circle with a hole in the middle) and arrived at the Laurent series.
\[f(z) = \sum_{n = -\infty}^{\infty} c_n (z - a)^n\]Now what if we generalize the domain beyong an open disk or annular region?
Region with holes
Suppose $f(z)$ is a holomorphic function in a multiply connected region $\Omega$, or in less precise words, a region with holes. Let $K$ be a compact (closed and bounded) set within that region (see Figure 1).
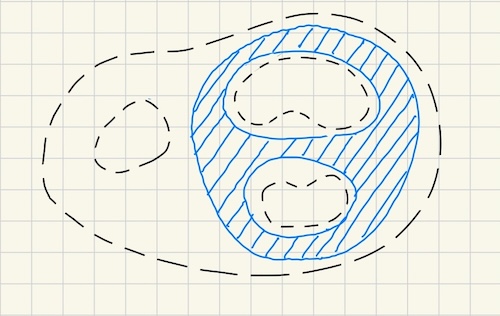
What Runge’s theorem tells us is that we can approximate $f(z)$ by rational functions in $K$. We’ll state it more precisely but first, let’s start with some lemmas to gain an intuition on why it is possible.
Lemma 1. Let $f(z)$ be a holomorphic function in a multiply connected region $\Omega$ and $K$ a compact subset of that region.
Then there exists a sequence of functions $(f_n(z))$ that converges uniformily to $f(z)$ in $K$. Such that $f_n(z)$ is a series of the form $\frac{c}{\alpha - z}$ for constants $c$ and $\alpha$ and $\alpha \not \in K$.
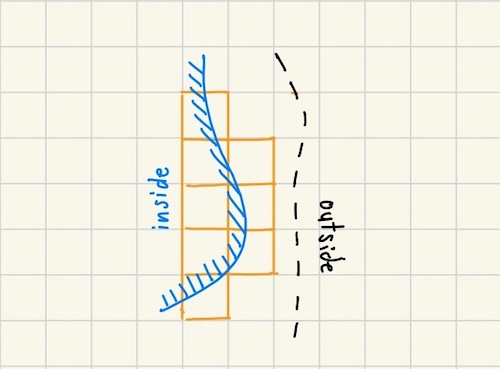
Let $C_1, \cdots, C_J$ the set of squares that have at least one point of $K$. Since each of these squares is contained in $\Omega$ in which $f(z)$ is holomorphic, we can apply Cauchy's integral formula [2] and get: $$f(z) = \frac{1}{2\pi i}\int_{C_j} \frac{f(w)}{w - z}dw$$ For $z \not \in C_j$, the function $f(z)/(w - z)$ is holomorphic and hence the integral over $C_j$ would be 0. Thus we can also write: $$f(z) = \frac{1}{2\pi i} \sum_{j=1}^{J} \int_{C_j} \frac{f(w)}{w - z}dw$$ Edges that are shared by two squares will cancel out because they're in opposite direction, so we can consider the set of "outer" edges $E_j$ instead: $$(1) \quad f(z) = \frac{1}{2\pi i} \sum_{j=1}^{J'} \int_{E_j} \frac{f(w)}{w - z}dw$$ which has the advantage of being an orthogonal line segment. We not make the observation that no $z \in K$ belongs to any of these edges. If they did they would belong to two or more squares and their corresponding edges would have been cancelled out.
It's possible to show that we can approximate the integral $$I = \int_{0}^{1} F(t)dt$$ where $F(t): [0, 1] \rightarrow \mathbb{C}$, by the discrete sum: $$S_N = \frac{1}{N} \sum_{n = 0}^{N-1} F(n/N)$$ In particular we have that $S_N$ converges uniformily to $I$. Now, we wish to prove that $$\int_{E_j} \frac{f(w)}{w - z}dw$$ can be approximated by a discrete sum as well. First we parametrize it by the continuous function $\phi_j: [0, 1] \rightarrow E_j$: $$\int_{0}^{1} \frac{f(\phi_j(t))}{\phi_j(t) - z}dt$$ Then we define $$F(t) = \frac{f(\phi_j(t))}{\phi_j(t) - z}$$ and claim that it's continuous, so we can apply the observation above and that the integral is approximateable by $$\frac{1}{N} \sum_{n = 0}^{N-1} F(n/N)$$ or $$\frac{1}{N} \sum_{n = 0}^{N-1} \frac{f(\phi_j(n/N))}{\phi_j(n/N) - z}$$ Now define: $$f_N(z) = \frac{1}{2\pi i} \frac{1}{N} \sum_{j=1}^{J'} \sum_{n = 0}^{N-1} \frac{f(\phi_j(n/N))}{\phi_j(n/N) - z}$$ So we can now claim that $f_N(z)$ converges uniformily to $f(z)$ (from $(1)$). The values $\phi_j(n/N)$ and $f(\phi_j(n/N))$ are independent of $z$, so we conlude that $f(z)$ can be approximated by a sum of functions of the form $$\frac{c}{\alpha - z}$$ For constants $c$ and $\alpha$. We also have that $\alpha \not \in K$ because $\alpha = \phi_j(n/N)$ is a point in $E_j$ and we observed that no point in $K$ belongs to $E_j$.
QED.
Let $A$ be the set of $\alpha$ that appears in any terms $\frac{c}{\alpha - z}$ of the approximating series. From the construct used in the proof of Lemma 1, we can conclude that each $A \subset \Omega \setminus K$ (because, as we’ve seen, $\alpha$ belongs to an edge of a square contained in $\Omega$).
If $K$ has holes, then $\mathbb{C} \setminus K$ is a set of connected components $C_i$: one for each hole of $K$ and the unbounded one, which we call $C_0$.
By the same construct we also have that there’s at least one point from the component $C_i$ in $A$. That’s because there’s also a “gap” between $\Omega$ and $K$ for holes and thus a square edge must be present in that gap (refer to Figure 1).
We might conclude that $A$ also forms the set of poles of $f_n(z)$, but the next lemma claims that if $\alpha \in C_0$, then $\frac{c}{\alpha - z}$ can be approximated by polynomials.
Lemma 2. Let $C_0$ be the unbounded region of $\mathbb{C} \setminus K$. Then, if $\alpha \in C_0$ and $c$ a constant, the expression $\frac{c}{\alpha - z}$ can be approximated by polynomials for $z \in K$.
It's then possible to show that for any $\beta$ sufficiently close to $\alpha$ that $\beta$ is also in $S$. Since $C_0$ is path-connected, by transitivity, any point in $C_0$ is also in $S$.
What Lemma 2 tells us is that $\alpha \in C_0$ is not really a pole for the fractions $\frac{c}{\alpha - z}$ since we can write it as a polynomial. So the only poles of $f_n(z)$ are points from the bounded components $C_i$.
Now let $\alpha$ be a point of $A$ belonging to a bounded component $C_i$. Lemma 3 tells us we can approximate $\frac{1}{\alpha - z}$ by another rational function where the only pole is some other point in $\beta \in C_i$.
Lemma 3. Let $\alpha \in C_i$. Then we can approximate $\frac{1}{\alpha - z}$ by a rational function where the only pole is $\beta \in C_i$.
By applying this approximation transivitely, we can generalize this to any $\beta \in C_i$, because it's a path connected component.
QED.
So from each bounded connected component $C_i$ we can choose a single representative point $\alpha$, sort of like a base, and approximate each term $\frac{1}{\alpha - z}$ as a rational function where the only poles are $\alpha$.
This leads to Runge’s Theorem:
Theorem 3. Let $f(z)$ be an holomorphic function in $\Omega$. Let $K$ be a compact subset of $\Omega$. Let $C_i$ be the bounded connected components of $\mathbb{C} \setminus K$ and let $A$ be a set containing at least one point from each $C_i$.
Then $f(z)$ can be approximated by a rational function where the only poles are those in $A$.
Unfortunately the theorem only shows the existence of such a function but not how to construct it, as opposed to the Taylor series or Laurent series approximations.
Conclusion
In this post we learned that a function can be approximated by a rational function which might contain poles.
If the domain of $f(z)$ contains holes, we can actually choose one point for each hole and prove that a rational function with poles corresponding to those points exist, but we don’t have a way to find it!
