kuniga.me > NP-Incompleteness > Buffon's Needle
Buffon's Needle
16 Aug 2022
In his book How Not To Be Wrong, Jordan Ellenberg discusses the Buffon’s Needle as follows. Suppose we’re given a needle of length $\ell$ and we drop it in a hardwood floor, consisting of vertical slats of width $\ell$. What is the chance it will cross slats?

In this post we’ll explore a solution to this problem and provide an algorithm to simulate it.
Mathematical Formulation
To formalize the problem, we’ll assume the needle is a line segment of length $\ell$ and the hardwood floor consists of an infinite plane with parallel lines $\ell$ units of distance apart. We want to compute the probability $p$ of the line segment intersecting any line.
An observation is that the segment can cross at most one line. In theory there’s a possibility the needle falls perfectly horizontal but the probability of that happening is infinitesimal.
Simulation
We can simulate a random segment drop as follows: we choose a point in the plane at random and let that be the center $c = (c_x, c_y)$ of a unit circle, where $0 \le c_x \le 1$ (the value of $c_y$ does not matter). We then pick a random point in the circumference $b = (b_x, b_y)$ of such circle.
To determine whether it crosses a line we just need to check whether the endpoints of the segments are on different slats. Note that only the $x$ values matter for this and we just need to verify whether $\lfloor \frac{b_x}{\ell} \rfloor = \lfloor \frac{c_x}{\ell} \rfloor$.
We just saw in the post Random Points in Circumference how to compute points in the circumference without explicit use of angles. Given random variables $X, Y$ uniformily distributed on $[-1, 1]$ and satisfying $X^2 + Y^2 \le 1$, a point in the circumference is given by:
\[X' = \frac{X^2 - Y^2}{X^2 + Y^2}\\ \\ Y' = \frac{2XY}{X^2 + Y^2}\]We then get $c_x$ and $c_y$ from uniformily distributed random variables $C_X$ and $C_Y$. $b_x$ can be obtained via:
\[\frac{X^2 - Y^2}{X^2 + Y^2} + C_X\]And $b_y$ via:
\[\frac{2XY}{X^2 + Y^2} + C_Y\]Computing the Probability
We can compute the probability of the segment crossing a line geometrically. Recall from Random Points in Circumference that we compute the propability of random variables $X, Y$ uniformily distributed on $[-1, 1]$ satisfying $X^2 + Y^2 \le 1$ as $\pi/4$ by the ratio of the areas of a unit circle over that of a square with size 2.
First we observe that we don’t need to consider $c_y$ in this analysis and we can assume $0 \le c_x \le 1$ by noting it doesn’t matter in which slat it lands on but only the relative position from the left side of the slat. So we will use random variables $X, Y$ uniformily distributed on $[-1, 1]$ and $C_X$ uniformily distributed on $[0, 1]$.
Since we’re using 3 random variables, we need to do a ratio of volumes to compute the probability. The denominator of the ratio is the volume of the samples under consideration, more precisely $X^2 + Y^2 \le 1$ and $0 \le C_X \le 1$, which is a cilinder with volume $\pi$.
The numerator of the ratio is more complicated. Let’s look at one slice of the cilinder for $C_X = z$, which is a circle. Consider a point $(x, y)$ in this circle, which can be writen in polar coordinates $(r, \theta)$. By definition $b_x = \cos \theta + z$.
Let’s consider two cases: the segment $\overline{cb}$ is leaning forward, in which case $0 \le \theta \le \frac{\pi}{2}$ or $\frac{3\pi}{2} \le \theta \le 2\pi$ or leaning backward, where $\frac{\pi}{2} \le \theta \le \frac{3\pi}{2}$. Now we note there’s symmetry on the $y$-axis so it suffices to look at angles $0 \le \theta \le \pi$.
If it’s leaning forward, let $\theta_f$ be the angle such that $\cos \theta_f + z = 1$. If we lean the segment more forward (i.e. towards a horizontal position), moving the angle $\theta_f$ towards 0, the crossing will still happen.
So the samples in which a crossing happens when leaning forwars is a sector from angles $0$ to $\theta_f = \cos^{-1} (1 - z)$. The area of a sector with angle $\alpha$ is $\frac{\alpha}{2}$, so the area of the sector is
\[\frac{\cos^{-1} (1 - z)}{2}\]but accounting for the $y$-axis symmetry, we multiply it by 2:
\[(1) \quad \cos^{-1} (1 - z)\]A similar argument gives us the area of the sector when leaning backwards:
\[(2) \quad \cos^{-1} (z)\]The sector corresponding to samples “leaning forward” that crosses the line is shown in green in Figure 2, while the one corresponding to “leaning backward” is shown in red.
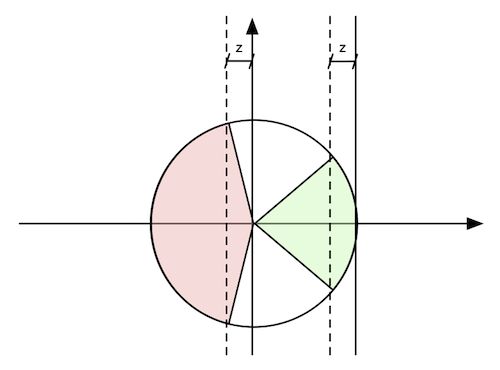
If we wish to compute the volume of the points corresponding to a crossing, we thus need to integrate the area of these sectors over $z$. We note that (1) and (2) are the same if we flip the direction of integration from $z = 0 \rightarrow 1$ to $z = 1 \rightarrow 0$, so for the purpose of volume calculation we can do:
\[2 \int_{z=0}^{1} \cos^{-1} (z) dz\]Which is
\[2 \left( z \cos^{-1}(z) - \sqrt{1 - z^2} + C \rvert_{z = 0}^{1} \right) = 2\]So the volume of the sectors is 2 and thus the probability of a segment crossing a line is $\frac{2}{\pi}$.
Buffon’s Noodle
There’s a very elegant solution that doesn’t require solving an explicit integral and it’s attributed to Joseph-Émile Barbier. It relies on the linearity of expectation, that is $E[X_1 + X_2] = E[X_1] + E[X_2]$, which holds even if $X_1$ and $X_2$ are not independent.
Let’s generalize a bit and suppose we are want to compute the expected number $E_S$ of crossings given a segment of length $\ell$, not necessarily of length 1 as above.
Suppose we split the segment into two equal parts. Since they’re identical, independently they have the same probability of crossing a line and hence the same expected value, say $e’$.
We can thus write the expected value $E_S$ as $E_S = 2 e’$. If we keep dividing into ever smaller parts, say $N$ segments of length $\delta_\ell$ (where $\ell = \delta_\ell N$) and expected value $\epsilon$, then:
\[E_S = \sum_{i = 1}^{N} \epsilon = N \epsilon = \ell \frac{\epsilon}{\delta_\ell}\]Let $x$ be a point in the segment and $f(x)$ some scalar function of $x$. We can pretend $\epsilon$ is the difference between $f$ evaluated at $x$ and a point in the neighborhood $x + \delta_\ell$, that is: $\epsilon = f(x + \delta_\ell) - f(x)$. If we take the limit:
\[\lim_{\delta_\ell \rightarrow 0} \frac{f(x + \delta_\ell) - f(x)}{\delta_\ell}\]We end up with the derivative $\frac{df(x)}{d\ell}$ and
\[E_S = \ell \frac{df(x)}{d\ell}\]Since for sub-segments of same lenght we have the same expected value, the derivative is the same no matter $x$, which formalizes our intuition that $E_S$ is proportional to $\ell$:
\[E_S = k \ell\]So we just need to find the constant $k$.
The big leap is that this process works for any differentiable curve, not necessarily a straight line and that’s why this problem is called Buffon’s noodle. One of such curves is the circle with diameter 1. Its circumference is $\pi$, so its expected number of crossing, say $E_C$, is given by $E_C = k \pi$. However, such a circle always crosses lines exactly twice so $E_C = 2$.
This allows us computing $k = \frac{2}{\pi}$. Since in our original problem $\ell = 1$, $E_S$ is also $\frac{2}{\pi}$ as we demonstated previously.
Conclusion
In this post we assumed the needle length $\ell$ and the slat width $w$ are the same. However, much of the same arguments apply to the case where $\ell \le w$, but not if $\ell \gt w$. The key difference is that when $\ell \le w$, a segment can only cross slats at most once, so the expectated value is equal to the probability.
For $\ell \gt w$ we can still determine the expected value which is what the Buffon’s Noodle problem solves.
The Buffon’s needle problem led me to ponder about generating points on the circumference and write a preliminary post [4].
It also found it nice that the recent insights led me to come up with a proof the probability of the Buffon’s needle via volume ratios which is also described in Using elementary calculus in Wikipedia [2].
