kuniga.me > NP-Incompleteness > Partition Matroids

Partition Matroids

12 Dec 2022

In this post we’ll learn about partition matroids, as well as matching and traversal matroids.

This is a continuation of a topic I started over 9 years ago, when we discussed matroids, so it’s worth a recap.

Matroid Definitions

Let \(E\) be a set of elements and \(\cal I\) a family of subsets of \(E\) (family here has the meaning of a set of elements that share some properties and it’s also clearer than using ‘set of subsets’). Let \(M = (E, \cal I)\) and consider the following properties:

1) \(\emptyset \in \cal I\) and if a subset \(I \in \cal I\), then all subsets of \(I\) belong to \(\cal I\) as well.

2) If \(I_p \in {\cal I}\) with \(\mid I_p \mid = p\) and \(I_{p+1} \in {\cal I}\) with \(\mid I_{p+1}\mid = p+1\), then there is an element \(e \in I_{p+1} \setminus I_{p}\) such that $I_p + e \in {\cal I}$. (Henceforth, by abuse of notation, when we say \(I + e\) we mean \(I \cup \{e\}\)).

If \(M\) satisfies both (1) and (2), we say that \(M\) is a matroid.

Each element in \(\cal I\) is called an independent set. A subset of $E$ not in $\cal I$ is called a dependent set. If there’s no other set containing \(I\) in \(\cal I\) we say it’s a maximal independent set.

Additional Definitions and Results

Symmetric difference of sets. Consider sets $S$ and $T$. The symmetric difference of $S$ and $T$ is a set that contains only elements from $S$ or $T$ but not both and is denoted by $S \oplus T$. In other words:

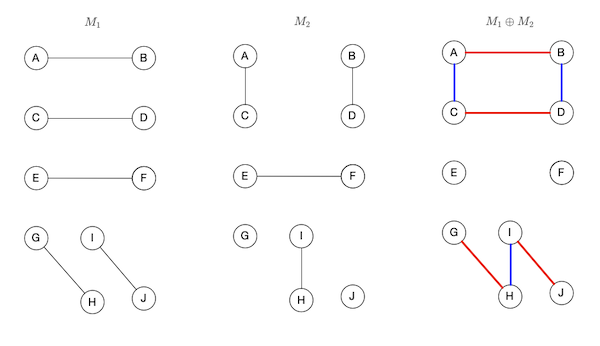
\[S \oplus T = (S \cup T) \setminus (S \cap T)\]

Lemma 1. Let $M_1$ and $M_2$ be two matchings in a graph $G(V, E)$. The symmetric difference $M_1 \oplus M_2$ is a set of paths and cycles with alternating edges from $M_1$ and $M_2$.

Proof. First we observe that in $M_1 \oplus M_2$, each vertex has degree at most 2. Having a degree greater than 2 would imply 3 edges being incident to it, which would mean two edges from either $M_1$ or $M_2$ incident to it, which cannot be since they’re matchings.

For vertices of degree exactly 2, its incident edges must come from different matches, for otherwise we’d have two edges from one matching incident to the same vertex.

Thus, the only type of graphs that can be formed are paths and cycles and the edges along them are alternating. For cycles, it also implies they even even length. QED.

Matching Matroid

Theorem 2. Let $G(V, E)$ be a graph and let $U$ be a subset of the set of vertices $V$. Let $I \subseteq U$ be such that there exists a matching $X$ in $G(V, E)$ such it covers $I$ (i.e. every vertex in $I$ belongs to an edge in $X$). Let $\cal{I}$ be the collection of all such $I$. Then $M(U, \cal I)$ is a matroid.

Proof. We need to show that $M(U, \cal I)$ satisfies conditions (1) and (2) of the matroid definition.

Let’s start with condition (1). If $I = \emptyset$ it’s vacuously covered. If $I$ is coverted by a matching $X$, then any of its subsets are also covered by the same matching, so they also belong to $\cal I$.

Now to condition (2). Let $I_p$ and $I_{p+1}$ any two vertex sets in $\cal I$ of sizes $p$ and $p+1$ respectively. We need to prove that there exists $v \in I_{p+1} \setminus I_p$ such that $I_p + v \in {\cal I}$, or that there exists some matching that covers $I_p + v$.

Let $X_p$ and $X_{p+1}$ any matches that cover $I_p$ and $I_{p+1}$ respectively. First suppose there is $v \in I_{p+1} \setminus I_p$ such that $X_p$ covers $v$. Then it also covers $I_p + v$, so $I_p + v \in {\cal I}$ and we’re done.

Otherwise, assume no $v \in I_{p+1} \setminus I_p$ is covered by $X_p$ (hypothesis $H_1$). Consider the symmetric difference of the matchings $X_p$ and $X_{p+1}$. Lemma 1 states that it’s a collection of alternating cycles and paths. Let’s consider some cases individually.

1) Alternating cycles. In such case every vertex in the cycle is covered by an edge from both $X_{p}$ and $X_{p+1}$. We claim that the number of vertices from $I_p$ is greater or equal to those from $I_{p+1}$. If this is not the case, one of the vertices is $v \in I_{p+1} \setminus I_p$, but since every vertex is covered by $X_{p}$ this violates $H_1$.

2) Alternating paths. Similar to the cycle case, the internal vertices (i.e. those of degree 2) are covered by an edge from both $X_{p}$ and $X_{p+1}$. Thus, by the same argument, the number of internal vertices coming from $I_p$ is greater or equal to those from $I_{p+1}$.

The only way to have more vertices from $I_{p+1}$ than $I_p$ in a path is by having it start with a vertex $v \in I_{p+1} \setminus I_p$, and an edge from $X_{p+1}$, and also having the same number of vertices from both $I_{p+1}$ and $I_{p+1}$, and finally having the last node not in $I_p$.

Since there are $p+1$ vertices in $I_{p+1}$ and $p$ in $I_{p}$, we must have this last scenario, i.e., there must exist an alternating path $P$ in $X_p \oplus X_{p+1}$ starting with $v$ and ending in a vertex not in $I_p$. This in turn implies that all vertices from $I_p$ are internal nodes of this path.

Thus if we remove from $X_p$ the edges $X_p \cap P$ and add edges from $X_{p+1} \cap P$, this resulting set of edges is a matching that covers the same internal nodes in $P$ but also the additional vertex $v$, which shows that $I_p + v \in {\cal I}$. QED.

Such matroid is called a matching matroid.

Traversal Matroid

Let $Q = \curly{q_1, \cdots, q_m}$ be a family of (not necessarily distinct) subsets of a set $E = \curly{e_1, \cdots, e_n}$. A set $T = \curly{e_{j_1}, \cdots, e_{j_t}}$ for $0 \le t \le n$ is a partial traversal of $Q$ if there is a bijective function $f: \mathbb{N} \rightarrow \mathbb{N}$ such that $e_{j_k} \in q_{f(k)}$ for $k = 1, \cdots, t$. $T$ is a traversal if $t = m$. In other words, in a partial traversal we select one element (called representative) from $t$ of the subsets in $Q$, such that these elements are all distinct.

Suppose that given $Q$ and $E$ we want to find the largest partial traversal. We can model this problem as the maximum bipartite matching. The left partition contains a vertex $i$ corresponding to each $e_e \in E$ and the right partition contains a vertex $j$ for each $q_j \in Q$. There’s an edge $(i, j)$ if $e_i$ belongs to $q_j$. Let $M$ be a matching on such graph. The vertices on the left partition covered by $M$ represent a partial traversal, so a maximum matching corresponds to a maximum partial traversal.

In Theorem 2, let $G(V,E)$ be the bipartite graph defined from $E$ and $Q$ as shown in the reduction above. Let $U$ be the vertices on the left partition. Then $\cal{I}$ is formed by sets $I \in U$ which are covered by a matching, so $I$ is a partial traversal of $Q$. This special type of matroid is called a traversal matroid.

Partition Matroid

Let $E$ be a set and $\pi$ a partition that separates $E$ into $m$ disjoint subsets $B_1, \cdots, B_m$. Let $I$ be a subset of $E$ such that is doesn’t include more than $d_i$ elements from a given partition $B_i$.

We claim that the $I$ define above is a special case of a partial traversal. We let $Q$ be a family of subsets containing $d_i$ copies of $B_i$ for $i = 1, \cdots, m$. Then a partial traversal $T$ be a subset of $E$ where at most $d_i$ of its elements will “represent” a given $B_i$.

This special case of traversal matroid is called a partition matroid and we can denote it by $M_{\pi, d}(E, \cal{I})$. In many cases we have $d_i = 1$ for all $i$, in which case we can simply use $M_{\pi}(E, \cal{I})$.

Example: Partition Matroid Intersection

Let $G(V,A)$ be a directed graph. Consider a partition $\pi_1$ of edges based on their head vertex, that is, edges entering a vertex $v$ belong to the same partition. Symmetrically, consider a partition $\pi_1$ of edges based on their tail vertex.

Then in the partition matroid $M_{\pi_1}(A, {\cal I}_1)$, $I \in {\cal I}_1$ represents a subset of edges such that no two edges enter the same vertex.

Conversely, in $M_{\pi_2}(A, {\cal I}_2)$, $I \in {\cal I}_2$ correspond to a subset of edges such that no two edges exit the same vertex.

If we take the intersection of ${\cal I}_1$ and ${\cal I}_2$, then $I \in {\cal I}_1 \cap {\cal I}_2$ represents the subset of edges such that no two edges enter or exit the same vertex. This corresponds to directed cycles and paths.

Conclusion

This post contains mostly definitions and proofs of different types of matroid. Our main goal is to define partition matroids, which will be important for a future post.

Lawler’s book [1] is sparse with the proof details. In particular for the matching matroid proof, it claims without further details that if no $v \in I_{p+1} \setminus I_p$ is covered by $X_p$ then there must exist an alternating path $P$ in $X_p \oplus X_{p+1}$ starting with $v$ and ending in a vertex not in $I_p$. It took me a while to convince myself.

Related Posts

An Introduction to Matroids. In that post we also studied matching matroids but only provided a sketch of the proof for it. In this we provide a full proof.

References

• [1] Combinatorial Optimization: Networks and Matroids, Eugene Lawler.