Max Area Under a Histogram

kuniga.me > NP-Incompleteness > Max Area Under a Histogram

Max Area Under a Histogram

09 Jan 2021

This is a classic programming puzzle. Suppose we’re given an array of $n$ values reprenting the height $h_i \ge 0$ of bars in a histogram, for $i = 0, \cdots, n-1$. We want to find the largest rectangle that fits “inside” that histogram.

More formally, we’d like to find indices $l$ and $r$, $l \le r$ such that $(l - r + 1) \bar h$ is maximum, where $\bar h$ is the smallest $h_i$ for $i \in \curly{l, \cdots, r}$.

In this post we’ll describe an $O(n)$ algorithm that solves this problem.

Simple $O(n^2)$ Solution

The first observation we make is that any optimal rectangle must “touch” the top of one of the bars. If that wasn’t true, we could extend it a bit further and get a bigger rectangle.

This means we can consider each bar $i$ in turn and check the largest rectangle that “touches” the top of that bar, that is, has height $h_i$. We start with the rectangle as the bar itself, then we expand the width towards the left and right. How far can we go?

It’s easy to visualize we can keep expanding until we find a bar whose height is less than $h_i$. This gives us an $O(n^2)$ algorithm: for each $i$, find the closest $l < i$ whose height is less than $h_i$ and the closest $r > i$ whose height is less than $h_i$.

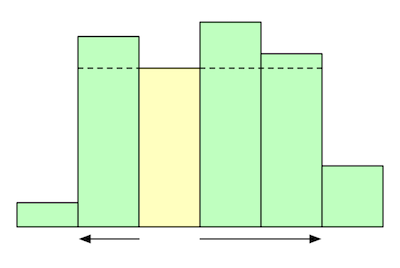
a diagram depicting a quantum circuit
Figure 1: Finding the left and right boundaries of the highlighted bar

We can assume that the first and last elements of the height array are sentinels with height -1, so we don’t have to worry about corner cases since there are always such $l$ and $r$.

The maximum area will be $(r - l - 1)*h_i$. For illustration purposes we provide the Python code:

def get_max_area_hist(h):
    max_a = 0
    h = [-1] + h + [-1] # sentinels
    for i in range(1, len(n) - 1):
        l = i - 1
        while h[l] >= h[i]:
            l -= 1

        r = i + 1
        while h[r] >= h[i]:
            r += 1

        max_a = max(max_a, h[i]*(r - l - 1))
    return max_a

$O(n)$ Solution with a Stack

We can get rid of the inner loops by using a stack $S$. The stack will contain the indexes of the bars and starts out containing the sentinel element at 0 ($S = [0]$). At iteration $i$, we pop all elements from the stack that are greater than $h_i$ and then add $i$. Let’s represent the elements of the stack as $S = [a_0, a_1, \cdots, a_m]$, where $a_m$ is the top of the stack. Let’s explore a few properties:

Property 1. The heights corresponding to the indices in the stack are sorted in non-decreasing order after each iteration. That is $h_{a_0} \le h_{a_1} \le \cdots, h_{a_m}$.

Proof. We can show this by induction. It’s clearly true for a single element. Now suppose the property holds at the beginning of iteration $i$. Before we insert $i$ at the top, we’ll remove all the indices whose heights are bigger than $h_i$. Let the resulting stack be $S = [a_0, a_1, \cdots, a_{m’}]$. By hypothesis $h_{a_0} \le h_{a_1} \le \cdots, h_{a_{m’}}$ and by constuction $h_i \ge h_{a_{m’}}$, so the property holds after the insertion of $i$. QED.

Property 2. For a given index $a_i$ in the stack ($i > 0$), $a_{i - 1}$ is the closest $l < a_{i}$ whose height is less than $h_{a_{i}}$.

Proof. Let $j$ be the index stored at the top of the stack right before inserting $i$. We want to show $j = l$. We first note that by construction $h_j < h_i$ and $j < i$. Suppose $j \neq l$. Then $j < l$ by the definition of $l$. So if $l$ is not at the top of the stack, it got popped out since it was added, but it can only be popped at iteration $l’ > l$ whose height is smaller than $h_l$, which is a contradiction, since $l’$ would be closer to $i$ and $h_{l’} < h_i$.

This holds as long as both $i$ and $l$ remain on the stack since their order never change. QED.

Property 3. If at iteration $i$ the index $j$ is popped from the stack, then $i$ is the closest $r > j$ whose height is less than $h_j$.

Proof. We know that $h_j > h_i$ because it was popped and $i > j$ by construction. It remains to show that $i$ is the closest index to $j$. Suppose it’s not, that there is $i > i’ > j$ such that $h_j > h_{i’}$. Since by Property 1 the heights in the stack are always in non-decreasing order, at iteration $i’$ it would have caused all elements on top of $j$ in $S$ to the popped and then $j$, but since $j$ is still in the stack, this cannot be so. QED.

Concluding, by Property 3, if $j$ is popped out in iteration $i$, then $r = i$. Moreover once $j$ is popped, the top stack happens to be $l$ by Property 2.

This leads to this algorithm:

def get_max_area_hist(h):
    max_a = 0
    h = [-1] + h + [-1] # sentinels
    stack = [0]
    for i in range(1, len(h)):
        while h[stack[-1]] > h[i]:
            j = stack.pop()
            l, r = i, stack[-1]
            max_a = max(max_a, h[j]*(l - r - 1))

        stack.append(i)

    return max_a

We still have an inner loop but we can argue that the amortized cost is $O(n)$: every iteration of the inner while loop removes an element from the stack, and we only add elements to the stack $O(n)$ times, so we only execute the inner loop $O(n)$ times.

Largest Submatrix of a Binary Matrix

Consider the following problem: we’re given a $n \times m$ binary matrix $B$ and we want to find the area of the largest rectangle that only contains 1s.

We will now show how to solve this problem in $O(nm)$. The idea is to find the largest rectangle that ends at row $i$, and then take the maximum accross all rows.

Suppose that the largest rectangle ending in row $i$ includes a given column $j$. The maximum height it can have is bounded by how many consecutive 1s there in previous rows for column $j$. If we call the length of such consecutive 1s $h_j$, we can now visualize these as heights of columns, so finding the largest rectangle ending in row $i$ can be reduced to finding the maximum area under a histogram, which we can do in $O(m)$.

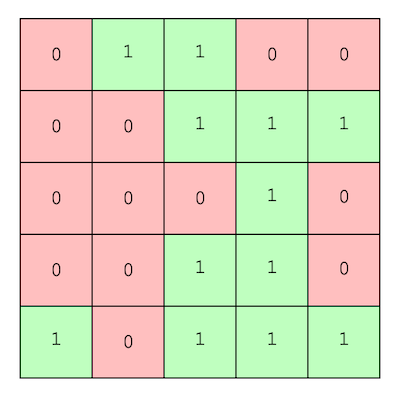
a diagram depicting a quantum circuit
Figure 2: 5 x 5 matrix. At the last row, he can visualize bars of histogram with heights: 1, 0, 2, 4, 1

How do we compute $h_j$ for row $i$? If we know the the “heights” of row $i-1$, say $h’$, we can compute it for $i$. Let $b_{ij}$ be the element in $B$ at row $i$ and column $j$. If $b_{ij} = 1$, then $h_j = h’_j + 1$. Otherwise, we break the chain of consecutive 1s, so $h_j = 0$.

def get_max_rectangle(b):
    max_a = 0
    hist = [0]*m
    for i in range(n):
        for j in range(m):
            if matrix[i][j] == 1:
                hist[j] += 1
            else:
                hist[j] = 0

        max_a = max(max_a, get_max_area_hist(hist))

It’s easy to see that the algorithm above is $O(nm)$.

Note that if the problem asked for the largest square, the problem is easier. Let $s_{ij}$ be the length of any side of the largest square that ends at row $i$ and column $j$ and we know how to comput it for $i’ = i - 1$ or $j’ = j - 1$. Then $s_{ij} = \min(s_{ij’}, s_{i’j}, s_{i’j’}) + 1$.

Conclusion

I remember seeing the “max area under histogram” problem a long time ago but I didn’t remember the solution. The use of a stack is very clever but not straightforward to see why it works.

References

Source code | RSS feed RSS Icon | Tags: combinatorial optimization puzzle