kuniga.me > NP-Incompleteness > Skip Lists in Python

Skip Lists in Python

25 Sep 2012

Skip list is a probabilistic data structure that allows efficient search, insertion and removal operations. It was invented by William Pugh [1] in 1989.

Other structures that have efficient operations are self-balancing binary trees, such as AVL, Red-black and splay tree. But they are often considered difficult to implement.

On the other hand, skip lists are much like multiple linked lists with some randomization.

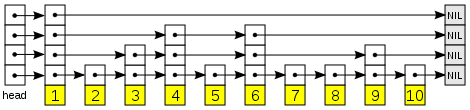
In the first level, we have a regular linked list with the elements sorted. Each element of this list has a probability \(p\) to be also present in the level above. The second level will probably contain fewer elements and each of these elements will also have a chance \(p\) to be on the third level, and so on. Figure 1 shows an example of a skip list.

We’ll implement a simple version of the skip list in python. To start, we define a skip list node. We’ll represent each level where the node appears by a list of pointers to the next nodes.

class SkipNode:
    def __init__(self, height = 0, elem = None):
        self.elem = elem
        self.next = [None]*height

Our skip list is just a sentinel skip node with height initially set to 0 and that stores a null element.

class SkipList:
    def __init__(self):
        self.head = SkipNode()

Now, let’s implement the search operation of this list.

Search

To search for an element \(q\) in a skip list we begin in the topmost level of the header. We go through the list in this level until we find node with the largest element that is smaller than \(q\).

We then go to the level below and search again for node with the largest element that is smaller than \(q\), but this time we began the search from the node we found in the level above.

When we find such node, we go down again and repeat this process until we reach the bottom level. The node \(x\) found in the bottom level will be the largest element that is smaller than \(q\) in the whole list and if \(q\) is in this list, it will be to the right of \(x\).

Also, we want to keep the nodes found in each level right before going down to the level below since it will make the insertion and deletion operations very simple.

This idea can be translated into the following code:

def updateList(self, elem):

    update = [None]*len(self.head.next)
    x = self.head

    for i in reversed(range(len(self.head.next))):
        while x.next[i] != None and \
            x.next[i].elem < elem:
            x = x.next[i]
        update[i] = x

    return update

It returns a list of nodes in each level that contains the greatest value that is smaller than elem.

The actual find function returns the node corresponding to the query element or None if it is not present in the skip list.

def find(self, elem, update = None):
    if update == None:
        update = self.updateList(elem)
    if len(update) > 0:
        candidate = update[0].next[0]
        if candidate != None and candidate.elem == elem:
            return candidate
    return None

Complexity

The complexity of the search is given by the following Theorem [2]:

Theorem: The number of moves in a search is \(O(\log n)\) with high probability.

By high probability we mean that we can set an arbitrarily high probability by increasing the constant hidden in the \(O()\) notation. The proof of this Theorem is sketched in Appendix A.

Insertion

The insertion consists in deciding the height of the new node, using randomHeight() and for each of the levels up to this height, insert this new node after the node specified in update.

def insert(self, elem):

    node = SkipNode(self.randomHeight(), elem)

    while len(self.head.next) < len(node.next):
        self.head.next.append(None)

    update = self.updateList(elem)
    if self.find(elem, update) == None:
        for i in range(len(node.next)):
            node.next[i] = update[i].next[i]
            update[i].next[i] = node

Deletion

The deletion is pretty much like the insertion, but now we delete the node found using find() from all levels in which it appears.

def remove(self, elem):

    update = self.updateList(elem)
    x = self.find(elem, update)
    if x != None:
        for i in range(len(x.next)):
            update[i].next[i] = x.next[i]
            if self.head.next[i] == None:

Note that for the sake of simplicity we do not resize head.next when the lists at top levels become empty. It does not change the theoretical complexity in the worst case, but in practice it may improve performance.

Computational Experiments

The complete implementation of skip list is available at Github as well as some test cases and a simple implementation of a linked list.

Our computational experiments consist in comparing the execution time for linked lists (\(O(n)\) per operation), our simple skip list (\(O(\log n)\) with high probability) and an implementation of a red-black tree (worst-case \(O(\log n)\) per operation).

We ran 10000 insertions in each of these structures with a random sequence, an increasing sequence and a decreasing sequence. We measure the CPU time in seconds:

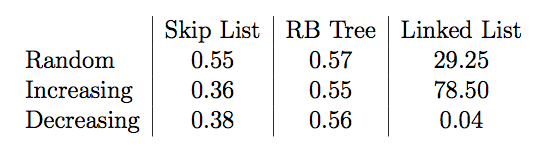
As we can see, for random input Red-black tree and Skip list have similar performance. For increasing and decreasing sequences, Skip list performed better than Red-black tree because the former is unaffected by the ordering of insertions, while the latter has to make many balancing operations in such cases.

As for linked lists, we can verify it’s much slower than the other two structures since it has \(O(n)\) worst case insertion time, but it outperforms when the elements are inserted in decreasing order since in this case insertion is \(O(1)\) :)

Conclusion

There is a combination of insertions and removals that may degenerate a skip list to a linked list, so the operations of searching, inserting and deleting become \(O(n)\) in the worst case scenario, though it is very unlikely to happen.

Demaine’s analysis [2] is stronger than Pugh’s [1]. The latter proves that the cost of the search is \(O(\log n)\) in average (i.e. expected cost) while the former proves it is \(O(\log n)\) for most of the cases.

References

• [1] Skip Lists: A Probabilistic Alternative to Balanced Trees - W. Pugh.
• [2] Introduction to Algorithms MIT - Lecture 12: Skip Lists - Erik Demaine

Appendix A: Proofs

In this section we present the proof of the Theorem stated in the post. Let \(L(n) = \log_{1/p} n\).

Before proving the Theorem, let’s prove the following Lemma:

Lemma: The number of levels in a skip list is \(O(L(n))\) with high probability.

Proof:

Let’s consider the error-probability, that is, the probability that there are more than \(c \cdot L(n)\) levels. We use the Boole’s inequality which says that for a set of events \(\{E_1, E_2, \cdots, E_k\}\):

Thus,

\(Pr\{ \mbox{max level } \ge c \cdot L(n) \} \le\) \(n \cdot Pr\{\mbox{node level } \ge c \cdot L(n) \}\)

Since each node height is given by a geometric distribution, we have that for some given level \(x\):

\(Pr\{\mbox{node level } < x\} = \sum_{i = 0}^{x - 1} Pr\{\mbox{node level } = x\} =\) \(\, (1 - p)\sum_{i = 0}^{x - 1} p^i = 1 - p^{k}\)

Also, \(p^{c \cdot L(n)} = p^{c \cdot \log_{1/p} n} = \frac{1}{n^{c}}\)

Finally,

Thus, for a sufficiently large constant \(c\), we have a very high probability, which proves the Lemma.

Theorem: The number of moves in a search is \(O(\log n)\) with high probability.

Proof:

Let’s prove that the number of moves in a search is \(O(L(n))\) with high probability.

First, consider the reversed path to find the returned element. This reversed path consists of up and left movements along the skip list. Note first that the number of up movements is bounded by the levels of the skip list.

An up movement is done with probability \(p\), which is the case that the current element has at least one more level. Otherwise a left movement is done with probability \(1 - p\).

Then, the length of the path is given by the number of movements until we reach \(c \cdot L(n)\) up movements. We claim that such number of movements is \(O(L(n))\) with high probability.

To prove our claim, let the number of movements be \(c'cL(n)\) for some other constant \(c'\). In [2], some combinatoric relations are used to show that

where \(\alpha = ((c'- 1) - L(c'e)) \cdot c\). We also have the converse:

Since \((c'- 1) > L(c'e)\) for sufficiently large values of \(c'\), we can choose \(c'\) to make \(\alpha\) arbitrarily large, which makes the probability above very high, proving the claim.

We conclude that the number of movements is \(O(cL(n)) = O(L(n))\) with high probability.

Source code | RSS feed | Tags: data structures, probabilistic algorithms, python