kuniga.me > NP-Incompleteness > Hypar

Hypar

23 Feb 2010

Hypar was coined by Erik Demaine [1], representing a hyperbolic paraboloid, and in this post we’ll study it.

This shape can be represented parametrically by the following equation:

\[(1) \quad z^2 = x^2 - y^2 \qquad \mbox{or} \qquad x = yz\]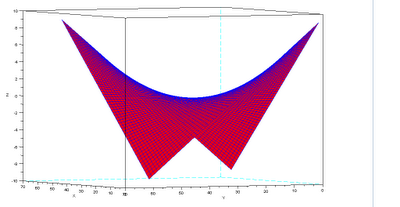

Demaine found out that it is possible to construct such a shape, which he calls hypar, through paper folding (origami). Figure 2 shows the step-by-step:

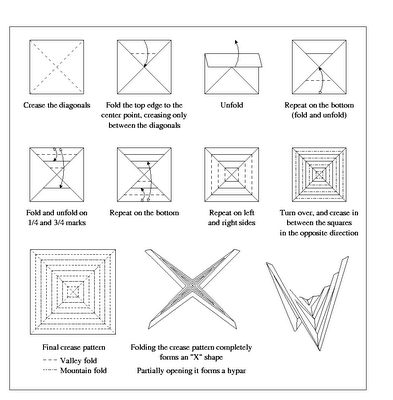
k-hat

By putting together several hypars, it is possible to form what Erik calls a $k$-hat. To do this, we must glue the sides of $k$ hipars so that the tallest end is in the center. Figure 3 shows a 4-hat:

Hyparhedra

Demaine’s paper [2] shows how to build any platonic solid from $k$-hats. The idea is straightforward: each face of the solid with $k$ sides becomes a $k$-hat and to join two faces we connect one end of one $k$-hat to the tip of the other.

Thus, a cube that has six four-sided faces, can be built with six 4-hats, that is, using 24 hypars.

Construction

With the help of Annelise, who, unlike me, has a talent for bending origami, we built the hyparhedra corresponding to a cube. Each hypar was folded using a 15cm x 15cm origami sheet and the result is in Figure 4.